题目内容
3．复数$\frac{3+4i}{{{{（1-i）}^2}}}$=（ ）| A． | $-2+\frac{3}{2}i$ | B． | $-2-\frac{3}{2}i$ | C． | $2+\frac{3}{2}i$ | D． | $2-\frac{3}{2}i$ |
分析 直接利用复数代数形式的乘除运算化简得答案．
解答 解：$\frac{3+4i}{{{{（1-i）}^2}}}$=$\frac{3+4i}{-2i}=\frac{（3+4i）i}{-2{i}^{2}}$=$\frac{-4+3i}{2}=-2+\frac{3}{2}i$．
故选：A．
点评 本题考查复数代数形式的乘除运算，是基础题．
练习册系列答案
相关题目
13．关于直线a，b，c以及平面α，β，给出下列命题：
①若a∥α，b∥α，则a∥b
②若a∥α，b⊥α，则a⊥b
③若a?α，b?α，且c⊥a，c⊥b，则c⊥α
④若a⊥α，a∥β，则α⊥β
其中正确的命题是（ ）
①若a∥α，b∥α，则a∥b
②若a∥α，b⊥α，则a⊥b
③若a?α，b?α，且c⊥a，c⊥b，则c⊥α
④若a⊥α，a∥β，则α⊥β
其中正确的命题是（ ）
| A． | ①② | B． | ②③ | C． | ②④ | D． | ①④ |
15．
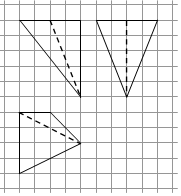如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，则该几何体的体积为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某四棱锥的三视图，则该几何体的体积为（ ）| A． | 15 | B． | 16 | C． | $\frac{50}{3}$ | D． | $\frac{53}{3}$ |
13．6人排成一排，若甲，乙，丙顺序一定，有多少种不同的排法（ ）
| A． | 6 | B． | 24 | C． | 120 | D． | 144 |