题目内容
若椭圆C1:
+
=1(a>b>0),过点Q(1,
)作圆C2:x2+y2=1的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若直线l与圆C2相切于点P,且交椭圆C1于点M,N,求证:∠MON是钝角.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若直线l与圆C2相切于点P,且交椭圆C1于点M,N,求证:∠MON是钝角.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由题意可知:c=1,kOQ=
,则kAB=-2,由此能求出椭圆的标准方程.
(Ⅱ)当直线l的斜率不存在时,由题意得∠MON是钝角;当直线l的斜率存在时,设直线l的方程为y=kx+m,M(x1,y1),N(x2,y2),与椭圆
+
=1,联立得到:(5k2+4)x2+10kmx+5m2-20=0,由此利用韦达定理结合已知条件能证明∠MON是钝角.
| 1 |
| 2 |
(Ⅱ)当直线l的斜率不存在时,由题意得∠MON是钝角;当直线l的斜率存在时,设直线l的方程为y=kx+m,M(x1,y1),N(x2,y2),与椭圆
| x2 |
| 5 |
| y2 |
| 4 |
解答:
(Ⅰ)解:由题意可知:c=1,kOQ=
,则kAB=-2,…(3分)
所以直线AB的方程是y=-2(x-1),即y=-2x+2,即b=2.…(5分)
所以a2=b2+c2=5,
故椭圆的标准方程为:
+
=1.…(7分)
(Ⅱ)证明:当直线l的斜率不存在时,由题意得∠MON是钝角,…(9分)
当直线l的斜率存在时,设直线l的方程为y=kx+m,M(x1,y1),N(x2,y2),
与椭圆
+
=1,联立得到:(5k2+4)x2+10kmx+5m2-20=0,
则
•
=x1x2+y1y2=(k2+1)x1x2+km(x1+x2)+m2,
由韦达定理,得x1+x2=-
,x1x2=
,
代入上式可以得到:
•
=(k2+1)x1x2+km(x1+x2)+m2
=
,…(12分)
因为直线l与圆C2相切,则
=1,
所以m2=1+k2,…(14分)
代入上式:
•
=
<0,
所以∠MON是钝角.…(15分)
| 1 |
| 2 |
所以直线AB的方程是y=-2(x-1),即y=-2x+2,即b=2.…(5分)
所以a2=b2+c2=5,
故椭圆的标准方程为:
| x2 |
| 5 |
| y2 |
| 4 |
(Ⅱ)证明:当直线l的斜率不存在时,由题意得∠MON是钝角,…(9分)
当直线l的斜率存在时,设直线l的方程为y=kx+m,M(x1,y1),N(x2,y2),
与椭圆
| x2 |
| 5 |
| y2 |
| 4 |
则
| OM |
| ON |
由韦达定理,得x1+x2=-
| 10km |
| 5k2+4 |
| 5m2-20 |
| 5k2+4 |
代入上式可以得到:
| OM |
| ON |
=
| 9m2-20(k2+1) |
| 5k2+4 |
因为直线l与圆C2相切,则
| |m| | ||
|
所以m2=1+k2,…(14分)
代入上式:
| OM |
| ON |
| 9m2-20(k2+1) |
| 5k2+4 |
所以∠MON是钝角.…(15分)
点评:本题考查椭圆的标准方程的求法,考查角为钝角的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
相关题目
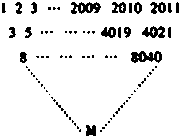 给定三角形数表如图所示,其中第一行各数依次是1,2,3,…,2009,2010,2011,从第二行起,每个数分别等于它上面一行左、右两数之和,设第i行第j个数为f(i,j)(i,j∈N*,i+j≤2012),则:f(8,1)=
给定三角形数表如图所示,其中第一行各数依次是1,2,3,…,2009,2010,2011,从第二行起,每个数分别等于它上面一行左、右两数之和,设第i行第j个数为f(i,j)(i,j∈N*,i+j≤2012),则:f(8,1)=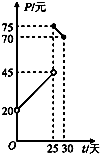 某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用如图表示,该商品在30天内日销售量Q(件)与时间t(天)之间的关系如下表:
某种商品在30天内每件的销售价格P(元)与时间t(天)的函数关系用如图表示,该商品在30天内日销售量Q(件)与时间t(天)之间的关系如下表: