题目内容
函数f(x)的图象如图,则f(x)的解析式可能是( )
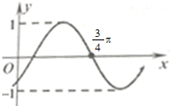

| A、f(x)=cos2x | ||||
B、f(x)=-sin(x+
| ||||
C、f(x)=cos(
| ||||
D、f(x)=sin(
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:利用正弦函数与余弦函数的图象与性质,对A、B、C、D四个选项逐一分析即可得到答案.
解答:
解:对于A,当x=0时,y=f(0)∈(-1,0),而f(0)=cos0=1∉(-1,0),故可排除A;
对于B,设f(x)=sin(ωx+φ),由图知,函数的周期
T<
,即
<
,
解得ω>
,可排除B;
对于C,当x=
时,f(
)=cos(
×
-
)=cosπ=-1≠0,即f(x)=cos(
x-
)不经过(
,0),故可排除C;
对于D,由以上分析知,
>
,且f(
)=sin(
×
-
)=sinπ=0,满足题意,故D正确.
故选:D.
对于B,设f(x)=sin(ωx+φ),由图知,函数的周期
| 1 |
| 2 |
| 3π |
| 4 |
| π |
| ω |
| 3π |
| 4 |
解得ω>
| 4 |
| 3 |
对于C,当x=
| 3π |
| 4 |
| 3π |
| 4 |
| 3 |
| 2 |
| 3π |
| 4 |
| π |
| 8 |
| 3 |
| 2 |
| π |
| 8 |
| 3π |
| 4 |
对于D,由以上分析知,
| 5 |
| 3 |
| 4 |
| 3 |
| 3π |
| 4 |
| 5 |
| 3 |
| 3π |
| 4 |
| π |
| 4 |
故选:D.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,着重考查正弦函数与余弦函数的图象与性质,考查排除法在解选择题中的应用,属于中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
设复数z1=1-i,z2=x+2i(x∈R),若
为实数,则x=( )
| z2 |
| z1 |
| A、-2 | B、-1 | C、1 | D、2 |
假设在5秒内的任何时刻,两条不相关的短信机会均等地进人同一部手机,若这两条短信进人手机的时间之差小于2秒,手机就会受到干扰,则手机受到干扰的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设变量x,y满足约束条件
,则z=x-3y的最大值为( )
|
| A、-4 | B、4 | C、3 | D、-3 |
已知i为虚数单位,若
=y+2i,x,y∈R,则复数x+yi=( )
| x-i |
| i |
| A、2+i | B、-2-i |
| C、l-2i | D、1+2i |
不等式
≥0的解集是( )
| 2-x |
| x-1 |
| A、(-∞,1)∪[2,+∞) |
| B、(-∞,1]∪[2,+∞) |
| C、[1,2] |
| D、(1,2] |
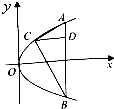 如图,直角三角形ABC的三个顶点在给定的抛物线y2=2px(p>0)上,斜边AB平行于y轴,则AB边上的高|CD|=
如图,直角三角形ABC的三个顶点在给定的抛物线y2=2px(p>0)上,斜边AB平行于y轴,则AB边上的高|CD|=