题目内容
假设在5秒内的任何时刻,两条不相关的短信机会均等地进人同一部手机,若这两条短信进人手机的时间之差小于2秒,手机就会受到干扰,则手机受到干扰的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:根据几何概型的概率公式求出对应的测度,即可得到结论.
解答:
 解:分别设两个互相独立的短信收到的时间为x,y.则所有事件集可表示为0≤x≤5,0≤y≤5.
解:分别设两个互相独立的短信收到的时间为x,y.则所有事件集可表示为0≤x≤5,0≤y≤5.
由题目得,如果手机受则到干扰的事件发生,必有|x-y|≤2.
三个不等式联立,则该事件即为x-y=2和y-x=2在0≤x≤5,0≤y≤5的正方形中围起来的图形
即图中阴影区域而所有事件的集合即为正方型面积52=25,
阴影部分的面积25-2×
(5-2)2=16,
所以阴影区域面积和正方形面积比值即为手机受到干扰的概率为
.
故选:C.
 解:分别设两个互相独立的短信收到的时间为x,y.则所有事件集可表示为0≤x≤5,0≤y≤5.
解:分别设两个互相独立的短信收到的时间为x,y.则所有事件集可表示为0≤x≤5,0≤y≤5.由题目得,如果手机受则到干扰的事件发生,必有|x-y|≤2.
三个不等式联立,则该事件即为x-y=2和y-x=2在0≤x≤5,0≤y≤5的正方形中围起来的图形
即图中阴影区域而所有事件的集合即为正方型面积52=25,
阴影部分的面积25-2×
| 1 |
| 2 |
所以阴影区域面积和正方形面积比值即为手机受到干扰的概率为
| 16 |
| 25 |
故选:C.
点评:本题主要考查几何概型的概率的计算,分别求出对应区域的面积是解决本题的关键,比较基础.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
复数z=
-(i-1)(i+1)的模是( )
| 1 |
| i |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
已知首项为1的等比数列{an}是摆动数列,Sn是{an}的前n项和,且
=5,则数列{
}的前5项和为( )
| S4 |
| S2 |
| 1 |
| an |
| A、31 | ||
B、
| ||
C、
| ||
| D、11 |
函数f(x)的图象如图,则f(x)的解析式可能是( )
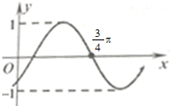

| A、f(x)=cos2x | ||||
B、f(x)=-sin(x+
| ||||
C、f(x)=cos(
| ||||
D、f(x)=sin(
|
 如图是求10!的程序框图,则在判断框内应填的条件可以是( )
如图是求10!的程序框图,则在判断框内应填的条件可以是( )| A、i<10? |
| B、i≤10? |
| C、i≤11? |
| D、i>10? |
一个几何体的三视图如图所示,则该几何体的外接球的体积为( )


A、4
| ||
| B、12π | ||
C、2
| ||
D、4
|
一个几何体的三视图如图所示,则这个几何体的表面积等于( )


| A、72 | B、66 | C、60 | D、30 |