题目内容
已知函数f(x)=
ax3+bx2+x+3,其中a≠0.
(1)当实数a,b满足什么条件时,函数f(x)存在极值?
(2)若a=1,函数f(x)在区间(0,1]上是增加的,求实数b的取值范围.
| 1 |
| 3 |
(1)当实数a,b满足什么条件时,函数f(x)存在极值?
(2)若a=1,函数f(x)在区间(0,1]上是增加的,求实数b的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:计算题,函数的性质及应用,导数的综合应用
分析:(1)求导f′(x)=ax2+2bx+1,由函数f(x)存在极值知ax2+2bx+1=0有两个不相等的实数根,从而求得;
(2)要使函数f(x)在区间(0,1]上是增加的,需使f′(x)=x2+2bx+1≥0在(0,1]上恒成立;故b≥-
-
在(0,1]上恒成立,设g(x)=-
-
,从而化为函数的最值问题.
(2)要使函数f(x)在区间(0,1]上是增加的,需使f′(x)=x2+2bx+1≥0在(0,1]上恒成立;故b≥-
| x |
| 2 |
| 1 |
| 2x |
| x |
| 2 |
| 1 |
| 2x |
解答:
解:(1)由已知得,f′(x)=ax2+2bx+1,
由函数f(x)存在极值知,
ax2+2bx+1=0有两个不相等的实数根,
故△=4b2-4a>0,
故b2>a;
即满足b2>a时,函数f(x)存在极值;
(2)由题意,f(x)=
x3+bx2+x+3,f′(x)=x2+2bx+1;
要使函数f(x)在区间(0,1]上是增加的,
需使f′(x)=x2+2bx+1≥0在(0,1]上恒成立;
故b≥-
-
在(0,1]上恒成立,
设g(x)=-
-
,则g′(x)=
-
≥0,
故g(x)=-
-
在(0,1]上是增函数,
故当x=1时,gmax(x)=g(1)=-1;
故b≥-1;
即实数b的取值范围为[-1,+∞).
由函数f(x)存在极值知,
ax2+2bx+1=0有两个不相等的实数根,
故△=4b2-4a>0,
故b2>a;
即满足b2>a时,函数f(x)存在极值;
(2)由题意,f(x)=
| 1 |
| 3 |
要使函数f(x)在区间(0,1]上是增加的,
需使f′(x)=x2+2bx+1≥0在(0,1]上恒成立;
故b≥-
| x |
| 2 |
| 1 |
| 2x |
设g(x)=-
| x |
| 2 |
| 1 |
| 2x |
| 1 |
| 2x2 |
| 1 |
| 2 |
故g(x)=-
| x |
| 2 |
| 1 |
| 2x |
故当x=1时,gmax(x)=g(1)=-1;
故b≥-1;
即实数b的取值范围为[-1,+∞).
点评:本题考查了导数的综合应用及恒成立问题,属于中档题.

练习册系列答案
相关题目
函数f(x)=ax-1(a>0且a≠1)恒过定点M,直线y=kx-2k+3(k∈R)恒过定点N,则直线MN的斜率为( )
| A、-3 | B、-2 | C、2 | D、3 |
某品牌香水瓶的三视图如图(单位:cm),则该几何体的表面积为( )
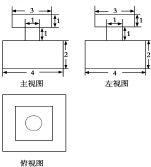

A、(95-
| ||
B、(94-
| ||
C、(94+
| ||
D、(95+
|
空间几何体的三视图如图所示,则该几何体的表面积和体积分别为( )


A、6+2
| ||
B、8+2
| ||
C、8+2
| ||
D、6+2
|