题目内容
已知M(a,2)是抛物线y2=2x上的一点,倾斜角为锐角的直线MP,MQ分别与抛物线交于P,Q两点,且直线MP,MQ的斜率之积为0.25,则直线PQ斜率的最大值是 .
考点:直线与圆锥曲线的关系
专题:圆锥曲线中的最值与范围问题
分析:由已知得M(2,2),设PM的斜率为k(k>0),则MQ的斜率为
,直线PM的方程为y-2=k(x-2),代入抛物线y2=2x,得y2-
+
-4=0,从而P(2(
-1)2,
-2),同理Q(2(4k-1)2,2(4k-1)),由此能求出直线PQ的斜率的最大值.
| 1 |
| 4k |
| 2y |
| k |
| 4 |
| k |
| 1 |
| k |
| 2 |
| k |
解答:
解:∵M(a,2)是抛物线y2=2x上的一点,
∴2a=4,解得a=2,即M(2,2),
设PM的斜率为k(k>0),
∵且直线MP,MQ的斜率之积为0.25,∴MQ的斜率为
,
∴直线PM的方程为y-2=k(x-2),代入抛物线y2=2x,并消x,得:
y2-
+
-4=0,
∴此直线与抛物线交于P,M两点,∴2yP=
-4,
∴yP=
-2,∴P(2(
-1)2,
-2),
同理,Q点坐标为Q(2(4k-1)2,2(4k-1)),
∴PQ的斜率k=
=
≤
=
,
当且仅当4k=
,即k=
时,取等号,
∴直线PQ的斜率的最大值为
.
故答案为:
.
∴2a=4,解得a=2,即M(2,2),
设PM的斜率为k(k>0),
∵且直线MP,MQ的斜率之积为0.25,∴MQ的斜率为
| 1 |
| 4k |
∴直线PM的方程为y-2=k(x-2),代入抛物线y2=2x,并消x,得:
y2-
| 2y |
| k |
| 4 |
| k |
∴此直线与抛物线交于P,M两点,∴2yP=
| 4 |
| k |
∴yP=
| 2 |
| k |
| 1 |
| k |
| 2 |
| k |
同理,Q点坐标为Q(2(4k-1)2,2(4k-1)),
∴PQ的斜率k=
2(4k-1)-(
| ||
[2(4k-1)2]-[2(
|
=
| 1 | ||
4k+
|
≤
| 1 | ||||
2
|
| 1 |
| 2 |
当且仅当4k=
| 1 |
| k |
| 1 |
| 2 |
∴直线PQ的斜率的最大值为
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查直线的斜率的最大值的求法,是中档题,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=ax-1(a>0且a≠1)恒过定点M,直线y=kx-2k+3(k∈R)恒过定点N,则直线MN的斜率为( )
| A、-3 | B、-2 | C、2 | D、3 |
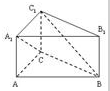 已知直三棱柱ABC--A1B1C1中,AB=4,AC=AA1=2,∠ACB=90°.
已知直三棱柱ABC--A1B1C1中,AB=4,AC=AA1=2,∠ACB=90°.