题目内容
7.已知向量$\overrightarrow a=({1,1})$,向量$\overrightarrow a$,$\overrightarrow b$的夹角为$\frac{π}{3}$,$\overrightarrow a•\overrightarrow b=\sqrt{2}$,则$|{\overrightarrow b}|$等于2.分析 可求出$|\overrightarrow{a}|=\sqrt{2}$,并且$\overrightarrow{a},\overrightarrow{b}$夹角已知,从而根据$\overrightarrow{a}•\overrightarrow{b}=\sqrt{2}$即可求出$|\overrightarrow{b}|$的值.
解答 解:$|\overrightarrow{a}|=\sqrt{2}$,$<\overrightarrow{a},\overrightarrow{b}>=\frac{π}{3}$;
∴$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos\frac{π}{3}$
=$\frac{\sqrt{2}}{2}|\overrightarrow{b}|$
=$\sqrt{2}$;
∴$|\overrightarrow{b}|=2$.
故答案为:2.
点评 考查根据向量坐标求向量长度的方法,以及向量数量积的计算公式.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
13.在Rt△ABC中,AB=AC=1,若一个椭圆经过A、B两点,它的一个焦点为点C,另一个焦点在边AB上,则这个椭圆的离心率为( )
| A. | $\frac{{2\sqrt{3}-\sqrt{6}}}{2}$ | B. | $\sqrt{2}-1$ | C. | $\frac{{\sqrt{6}-\sqrt{3}}}{2}$ | D. | $\sqrt{6}-\sqrt{3}$ |
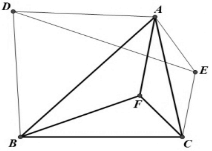 已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF.
已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF.