题目内容
13.在Rt△ABC中,AB=AC=1,若一个椭圆经过A、B两点,它的一个焦点为点C,另一个焦点在边AB上,则这个椭圆的离心率为( )| A. | $\frac{{2\sqrt{3}-\sqrt{6}}}{2}$ | B. | $\sqrt{2}-1$ | C. | $\frac{{\sqrt{6}-\sqrt{3}}}{2}$ | D. | $\sqrt{6}-\sqrt{3}$ |
分析 设另一焦点为D,则可再Rt△ABC中,根据勾股定理求得BC,进而根据椭圆的定义知AC+AB+BC=4a求得a.再利用AC+AD=2a求得AD最后在Rt△ACD中根据勾股定理求得CD,得到椭圆半焦距,进一步求得离心率.
解答 解:设另一焦点为D,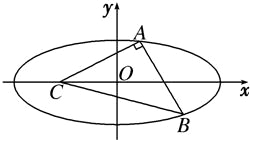
∵Rt△ABC中,AB=AC=1,
∴BC=$\sqrt{2}$,
∵AC+AD=2a,
∴AC+AB+BC=1+1+$\sqrt{2}$=4a,
∴a=$\frac{2+\sqrt{2}}{4}$,
又∵AC=1,∴AD=$\frac{\sqrt{2}}{2}$.
在Rt△ACD中焦距CD=$\sqrt{A{C}^{2}+A{D}^{2}}=\frac{\sqrt{6}}{2}$,
则c=$\frac{\sqrt{6}}{4}$,
∴$e=\frac{c}{a}=\frac{\frac{\sqrt{6}}{4}}{\frac{2+\sqrt{2}}{4}}=\frac{\sqrt{6}}{2+\sqrt{2}}=\sqrt{6}-\sqrt{3}$.
故选:D.
点评 本题主要考查了椭圆的简单性质和解三角形的应用.要理解好椭圆的定义和椭圆中短轴,长轴和焦距的关系是关键,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.函数y=$\frac{1+x}{1-x}$的图象大致为( )
| A. |  | B. |  | C. |  | D. |  |
1.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$上任意一点P,作与y轴平行的直线,交两渐近线于A,B两点,若$\overrightarrow{PA}•\overrightarrow{PB}=-\frac{a^2}{4}$,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{10}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
9.射线OA绕端点O逆时针旋转120°到达OB的位置,再顺时针旋转270°到达OC的位置,则∠AOC=( )
| A. | 150° | B. | -150° | C. | 390° | D. | -390° |
6.设x∈R,则“x>-1”是“x3>-1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充要条件 |
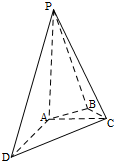 如图,在四棱锥P-ABCD中,PA丄平面ABCD,AB丄BC,∠BCA=45°,PA=AD=2,AC=1,DC=$\sqrt{5}$
如图,在四棱锥P-ABCD中,PA丄平面ABCD,AB丄BC,∠BCA=45°,PA=AD=2,AC=1,DC=$\sqrt{5}$