题目内容
15.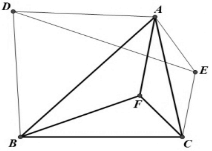 已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF.
已知,△ABC内有一点F,分别以AB、AC为底边向外作等腰三角形DAB、AEC,且∠BAD=∠BCF,∠ACE=∠CBF.求证:DE平分AF.
分析 如图,延长AD至M,延长AE至N,使得AD=MD,AE=EN,连接MB,NC、MN,作AP⊥MN,连接PB,PC,PF,利用等腰三角形与四点共圆的性质先证明点F在直线MN上,再利用三角形中位线定理即可证明.
解答 证明:如图,延长AD至M,延长AE至N,使得AD=MD,AE=EN,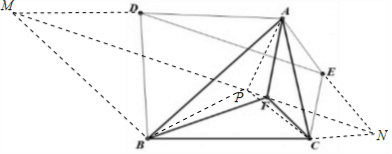
连接MB,NC、MN,作AP⊥MN,
连接PB,PC,PF,先证明点F在直线MN上,∵AD=MD=BD,∴MB⊥AB,
同理可得:CN⊥AC.又AP⊥MN,
可得A,M,B,P四点共圆,
可得A,N,C,P四点共圆,
可得:∠MPB=∠MAB=∠FCB,∠CPN=∠NAC=∠FBC,
∴∠BPC=180°-∠FBC-∠FCB,又∠BFPC=180°-∠PBC-∠FCB,
∴∠BPC=∠BFC,∴B,C,F,P四点共圆,
∴∠BPF+∠BCF=180°,∴∠BPM+∠BPF=180°,
∴M,P,F三点共线.即点F在直线MN上.
又AD=MD,AE=EN,
∴DE为△AMN的中位线,∴DE平分AF.
点评 本题考查了等腰三角形与四点共圆的性质、三角形中位线定理、三角形内角和定理,考查了推理能力与计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.过双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$上任意一点P,作与y轴平行的直线,交两渐近线于A,B两点,若$\overrightarrow{PA}•\overrightarrow{PB}=-\frac{a^2}{4}$,则该双曲线的离心率为( )
| A. | $\frac{{\sqrt{10}}}{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{6}}}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
6.设x∈R,则“x>-1”是“x3>-1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 既不充分也不必要条件 | D. | 充要条件 |
10.下列命题中的假命题是( )
| A. | ?x∈R,log2x=0 | B. | ?x∈R,cosx=1 | C. | ?x∈R,x2>0 | D. | ?x∈R,2x>0 |