题目内容
3.正四棱锥P-ABCD的侧棱长为$\sqrt{5}$,底面ABCD边长为2,E为AD的中点,则BD与PE所成角的余弦值为( )| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
分析 取AB的中点O,连接PO,OE,则OE∥BD,∠PEO是BD与PE所成角,利用余弦定理,即可求解.
解答  解:取AB的中点O,连接PO,OE,则OE∥BD,∠PEO是BD与PE所成角,
解:取AB的中点O,连接PO,OE,则OE∥BD,∠PEO是BD与PE所成角,
∵正四棱锥P-ABCD的侧棱长为$\sqrt{5}$,底面ABCD边长为2,
∴OE=$\sqrt{2}$,PO=PE=2,
∴cos∠PEO=$\frac{2+4-4}{2•\sqrt{2}•2}$=$\frac{\sqrt{2}}{4}$,
故选A.
点评 本题考查异面直线所成角,考查余弦定理的运用,确定∠PEO是BD与PE所成角是关键.

练习册系列答案
相关题目
13.调查某桑场采桑员桑毛虫皮炎发病情况结果如表:利用2×2列联表的独立性检验估计“患桑毛虫皮炎病与采桑”是否有关?认为两者有关系会犯错误的概率是多少?
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
| 分类 | 采桑 | 不采桑 | 总计 |
| 患者人数 | 18 | 12 | |
| 健康人数 | 5 | 78 | |
| 总计 |
| P(K2≥k0) | 0.050 | 0.010 | 0.001 |
| k0 | 3.841 | 6.635 | 10.828 |
14.设P,Q是两个集合,定义集合P-Q={x|x∈P,x∉Q}为P,Q的“差集”,已知$P=\left\{{x|1-\frac{2}{x}<0}\right\}$,Q={x||x-2|<1},那么Q-P等于( )
| A. | {x|0<x<1} | B. | {x|0<x≤1} | C. | {x|1≤x<2} | D. | {x|2≤x<3} |
11.正三棱柱ABC-A1B1C1中,D是AB的中点,CD等于$\sqrt{3}$,则顶点A1到平面CDC1的距离为( )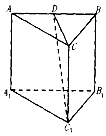

| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{2}$ |
8.已知三棱柱ABC-A1B1C1的侧棱垂直于底面,各顶点都在同一球面上,若该棱柱的体积为$\sqrt{3}$,AB=2,AC=1,∠BAC=60°,则此球的表面积是( )
| A. | 2π | B. | 4π | C. | 8π | D. | 10π |
15.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的焦距为2c(c>0),以原点O为圆心,a为半径作圆,过点$(\frac{a^2}{c}\;,\;0)$作该圆的两条切线,若这两条切线互相垂直,则椭圆的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
12.《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词,在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳》《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
| A. | 144种 | B. | 288种 | C. | 360种 | D. | 720种 |
13.湖面上漂着一个小球,湖水结冰后将球取出,冰面上留下了一个半径为4cm,深2cm的空穴,则该球表面积为( ) cm2.
| A. | 400π | B. | 300π | C. | 200π | D. | 100π |