题目内容
11.正三棱柱ABC-A1B1C1中,D是AB的中点,CD等于$\sqrt{3}$,则顶点A1到平面CDC1的距离为( )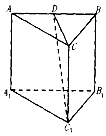
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{2}$ |
分析 证明A1B1⊥平面CDC1,即可求出顶点A1到平面CDC1的距离.
解答 解:由题意,D是AB的中点,CD等于$\sqrt{3}$,AB=2,
∵AB⊥CD,AB⊥C1C,CD∩C1C=C,
∴AB⊥平面CDC1,
∴A1B1⊥平面CDC1,
∴顶点A1到平面CDC1的距离为1
故选B.
点评 本题考查了求空间距离的方法,证明是A1B1⊥平面CDC1关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
19.完成下列抽样调查,较为合理的抽样方法依次是( )
①田传利老师从高一年级8名数学老师中抽取一名老师出月考题.
②我校高中三个年级共有2100人,其中高一800人、高二700人、高三600人,白凤库校长为了了解学生对数学的建议,拟抽取一个容量为300的样本;
③我校艺术中心有20排,每排有35个座位,在孟祥锋主任的报告中恰好坐满了同学,报告结束后,为了了解同学意见,学生处需要请20名同学进行座谈.
①田传利老师从高一年级8名数学老师中抽取一名老师出月考题.
②我校高中三个年级共有2100人,其中高一800人、高二700人、高三600人,白凤库校长为了了解学生对数学的建议,拟抽取一个容量为300的样本;
③我校艺术中心有20排,每排有35个座位,在孟祥锋主任的报告中恰好坐满了同学,报告结束后,为了了解同学意见,学生处需要请20名同学进行座谈.
| A. | ①简单随机抽样,②系统抽样,③分层抽样 | |
| B. | ①分层抽样,②系统抽样,③简单随机抽样 | |
| C. | ①系统抽样,②简单随机抽样,③分层抽样 | |
| D. | ①简单随机抽样,②分层抽样,③系统抽样 |
3.正四棱锥P-ABCD的侧棱长为$\sqrt{5}$,底面ABCD边长为2,E为AD的中点,则BD与PE所成角的余弦值为( )
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
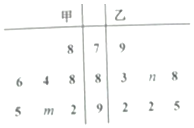 甲、乙两名同学在高一上学期7次物理考试成绩的茎叶图如图所示,其中甲成绩的平均数是88,乙学生的成绩中位数是89,则n-m的值是( )
甲、乙两名同学在高一上学期7次物理考试成绩的茎叶图如图所示,其中甲成绩的平均数是88,乙学生的成绩中位数是89,则n-m的值是( )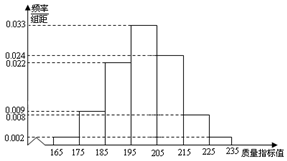 从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:求这500件产品质量指标值的样本平均数$\overline{x}$和样本方差s2(同一组数据用该区间的中点值作代表).
从某企业的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得如下频率分布直方图:求这500件产品质量指标值的样本平均数$\overline{x}$和样本方差s2(同一组数据用该区间的中点值作代表).