题目内容
设 函数f(x)=ax2+bx+1(a≠0,b∈R),若f(-1)=0,且对任意实数x(x∈R)不等式f(x)≥0恒成立.
(1)求实数a、b的值;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
(1)求实数a、b的值;
(2)在(1)的条件下,当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)由已知条件便得,
,所以便可得到(a-1)2≤0,所以只有(a-1)2=0,这样便求出a=1,b=2;
(2)先求出g(x)=x2+(2-k)x+1,该函数为二次函数,在对称轴一边有单调性,所以求出该函数对称轴为x=
,所以便有
≥2,或
≤-2,解不等式即得k的取值范围.
|
(2)先求出g(x)=x2+(2-k)x+1,该函数为二次函数,在对称轴一边有单调性,所以求出该函数对称轴为x=
| k-2 |
| 2 |
| k-2 |
| 2 |
| k-2 |
| 2 |
解答:
解:(1)由f(-1)=0得,a-b+1=0,∴b=a+1 ①;
∵对任意x∈R不等式f(x)≥0恒成立;
∴△=b2-4a≤0 ②;
①带入②得,(a-1)2≤0;
∴a=1,b=2;
(2)g(x)=x2+(2-k)x+1;
该函数对称轴为:x=
;
又g(x)在[-2,2]上是单调函数;
∴
≥2,或
≤-2;
∴k≥6,或k≤-2;
∴实数k的取值范围为(-∞,-2]∪[6,+∞).
∵对任意x∈R不等式f(x)≥0恒成立;
∴△=b2-4a≤0 ②;
①带入②得,(a-1)2≤0;
∴a=1,b=2;
(2)g(x)=x2+(2-k)x+1;
该函数对称轴为:x=
| k-2 |
| 2 |
又g(x)在[-2,2]上是单调函数;
∴
| k-2 |
| 2 |
| k-2 |
| 2 |
∴k≥6,或k≤-2;
∴实数k的取值范围为(-∞,-2]∪[6,+∞).
点评:考查一元二次不等式的解为R时判别式△的取值情况,以及二次函数的单调性和对称轴的关系.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
若g(x)=1-2x,f[g(x)]=(
)x,则f(4)=( )
| 1 |
| 3 |
A、
| ||
| B、-27 | ||
| C、9 | ||
D、3
|
甲,乙,丙三名运动员在某次测试中各射击20次,三人测试成绩的频率分布条形图分别如图1,图2和图3,若S甲,S乙,S丙分别表示他们测试成绩的标准差,则( )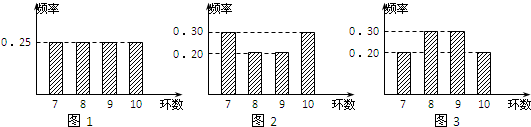

| A、S甲<S乙<S丙 |
| B、S甲<S丙<S乙, |
| C、S乙<S甲<S丙 |
| D、S丙<S甲<S乙 |
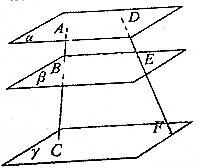 如图,直线AC、DF被三个平行平面α、β、γ所截:
如图,直线AC、DF被三个平行平面α、β、γ所截: