题目内容
已知F1、F2为双曲线C:x2-y2=1的左、右焦点,点P在双曲线C上,∠F1PF2=60°,则P到y轴的距离为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设|PF1|=m,|PF2|=n,不妨设m>n,化简求得mn=4,利用三角形面积相等求解.
解答:
解:设|PF1|=m,|PF2|=n,不妨设m>n,
可知a=1,b=1,c=
,
根据双曲线定义,
m-n=2a,即m2+n2-2mn=4,(1)
在△PF1F2中,根据余弦定理,
|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos60°,
即m2+n2-mn=8,(2)
(2)-(1)得,mn=4,
解得m=
+1,n=
-1,
设P到x轴的距离为h,则
mnsin60°=
×2
h,解得h=
,
设P到y轴的距离为g,则g=
-
=
=
;
故选:C.
可知a=1,b=1,c=
| 2 |
根据双曲线定义,
m-n=2a,即m2+n2-2mn=4,(1)
在△PF1F2中,根据余弦定理,
|F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos60°,
即m2+n2-mn=8,(2)
(2)-(1)得,mn=4,
解得m=
| 5 |
| 5 |
设P到x轴的距离为h,则
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
设P到y轴的距离为g,则g=
| m2-h2 |
| 2 |
(
|
| ||
| 2 |
故选:C.
点评:本题考查了双曲线的性质,结合余弦定理求出焦半径的长度,利用三角形的面积个数以及勾股定理求P到y轴距离,计算要准确,属于中档题.

练习册系列答案
相关题目
函数f(x)=x3+ax2+x在(0,+∞)有两个极值点,则实数a的取值范围是( )
A、(-∞,
| ||||
B、(-
| ||||
C、(
| ||||
D、(-∞,-
|
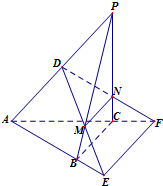 如图,在三棱锥P-ABC中,CP,CA,CB两两垂直且相等,过PA的中点D作平面α∥BC,且α分别交PB,PC于M,N,交AB,AC的延长线于E,F.
如图,在三棱锥P-ABC中,CP,CA,CB两两垂直且相等,过PA的中点D作平面α∥BC,且α分别交PB,PC于M,N,交AB,AC的延长线于E,F.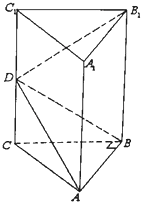 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点 函数f(x)=Asin(2x+φ),(A>0,|φ|<
函数f(x)=Asin(2x+φ),(A>0,|φ|<