题目内容
若直线l过点P（1，0）与双曲线x2-
=1只有一个公共点，则这样的直线有（ ）
| y2 |
| 4 |
| A、4条 | B、3条 | C、2条 | D、1条 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：因为点 （1，1）在双曲线x2-y2=3的渐近线上，所以结合双曲线的性质与图形可得过点（1，1）与双曲线公有一个公共点的直线有3条．
解答：
解：由题意可得：双曲线x2-
=1的渐近线方程为：y=±2x，
点P（1，0）是双曲线的顶点，故直线x=1与双曲线只有一个公共点；
过点P（1，0）平行于渐近线y=±2x时，直线L与双曲线只有一个公共点，有2条
所以，过P（1，0）的直线L与双曲线只有一个公共点，共有3条
故选：B．
| y2 |
| 4 |
点P（1，0）是双曲线的顶点，故直线x=1与双曲线只有一个公共点；
过点P（1，0）平行于渐近线y=±2x时，直线L与双曲线只有一个公共点，有2条
所以，过P（1，0）的直线L与双曲线只有一个公共点，共有3条
故选：B．
点评：本题以双曲线为载体，主要考查了直线与圆锥曲线的综合问题．突出考查了双曲线的几何性质．
练习册系列答案
相关题目
一个正四棱锥的五个顶点都在半径为1的球面上，其中底面的四个顶点在该球的一个大圆上，则该正四棱锥的体积是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
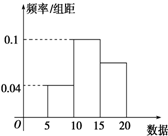如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数分别为（ ）| A、10 13 |
| B、12.5 12 |
| C、12.5 13 |
| D、10 15 |
满足等式sinx=lgx的实数x的个数为（ ）
| A、1 | B、2 | C、3 | D、5 |
已知函数f（x）=x3+ax2+6x-9有两个极值点x1，x2，且x12+x22=5，则a=（ ）
A、
| ||
B、-
| ||
C、±
| ||
| D、2 |
有600名同学参加夏令营，随机编号为000，001，…，599，现欲抽取50的样本，已知编号000～299的同学在第一营区，300～494的同学在第二营区，495-599的同学在第三营区，用系统抽样法，已知随机抽得的号码为002，则应从三个营区分别抽到的人数是（ ）
| A、26，16，8 |
| B、25，17，8 |
| C、25，16，9 |
| D、24，17，9 |
已知函数f（x）是R上的偶函数，且在（0，+∞）上单调递减，则f（a2-2a+3）与f（-2）的大小关系为（ ）
| A、f（a2-2a+3）＞f（-2） |
| B、f（a2-2a+3）＜f（-2） |
| C、f（a2-2a+3）≥f（-2） |
| D、f（a2-2a+3）≤f（-2） |
设函数f（x）=
，若f（a）＜-1，则实数a的取值范围是（ ）
|
| A、（-∞，-1） |
| B、（-∞，-1）∪[0，2） |
| C、（2，+∞） |
| D、（-∞，-1）∪（2，+∞） |
在△ABC中，已知sin2B-sin2C-sin2A=sinAsinC，则角B的大小为（ ）
| A、150° | B、30° |
| C、120° | D、60° |