题目内容
函数y=ex-x-2的单调递减区间是（ ）
| A、（-∞，0） |
| B、（0，+∞） |
| C、（-∞，1） |
| D、（-1，+∞） |
考点：利用导数研究函数的单调性
专题：计算题,导数的概念及应用
分析：求函数f（x）=ex-x-2的单调递减区间，可以先求函数f（x）=ex-x-2的导函数，然后由导函数式小于零求出x的范围，从而得到函数的减区间．
解答：
解：函数的定义域为（-∞，+∞），f′（x）=ex-1．
由f′（x）＜0，得ex-1＜0，ex＜1，∴x＜0，
所以函数的单调减区间为（-∞，0）．
故选：A．
由f′（x）＜0，得ex-1＜0，ex＜1，∴x＜0，
所以函数的单调减区间为（-∞，0）．
故选：A．
点评：本题考查了运用函数的导数研究函数的单调性，解答的关键是求出正确的函数导数．运用导函数求单调区间的方法是：由f′（x）＞0得到的x的区间为函数的增区间；由f′（x）＜0得到的x的区间为函数的减区间．
练习册系列答案
相关题目
在△ABC中，若cosA•cosB=sinA•sinB，则△ABC为（ ）
| A、锐角三角形 | B、直角三角形 |
| C、钝角三角形 | D、无法确定 |
一个算法的程序框图如图所示，若该程度输出的结果为
，则判断框①中应填入的条件是（ ）
| 7 |
| 12 |
| A、i＜5 | B、i＜4 |
| C、i＞4 | D、i≤3 |
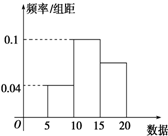如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数分别为（ ）| A、10 13 |
| B、12.5 12 |
| C、12.5 13 |
| D、10 15 |
满足等式sinx=lgx的实数x的个数为（ ）
| A、1 | B、2 | C、3 | D、5 |
已知函数f（x）=x3+ax2+6x-9有两个极值点x1，x2，且x12+x22=5，则a=（ ）
A、
| ||
B、-
| ||
C、±
| ||
| D、2 |
已知函数f（x）是R上的偶函数，且在（0，+∞）上单调递减，则f（a2-2a+3）与f（-2）的大小关系为（ ）
| A、f（a2-2a+3）＞f（-2） |
| B、f（a2-2a+3）＜f（-2） |
| C、f（a2-2a+3）≥f（-2） |
| D、f（a2-2a+3）≤f（-2） |
已知函数f（x）=sinx，下面结论错误的是（ ）
| A、f（x）的最小正周期是2π | ||||||||
B、f（x）在[0，
| ||||||||
C、f（x）[
| ||||||||
| D、f（x）的值域为[-1，1] |