题目内容
在等差数列{an}中,2a8+a9+a15=20,则数列{an}的前19项之和为( )
| A、98 | B、95 | C、93 | D、90 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由已知得2(a1+7d)+a1+8d+a1+14d=4a1+36d=20,从而数列{an}的前19项之和:S19=
(a1+a19)=
(2a1+18d)=
×
=95.
| 19 |
| 2 |
| 19 |
| 2 |
| 19 |
| 2 |
| 20 |
| 2 |
解答:
解:∵等差数列{an}中,2a8+a9+a15=20,
∴2(a1+7d)+a1+8d+a1+14d=4a1+36d=20,
∴数列{an}的前19项之和:
S19=
(a1+a19)=
(2a1+18d)=
×
=95.
故选:B.
∴2(a1+7d)+a1+8d+a1+14d=4a1+36d=20,
∴数列{an}的前19项之和:
S19=
| 19 |
| 2 |
| 19 |
| 2 |
| 19 |
| 2 |
| 20 |
| 2 |
故选:B.
点评:本题考查等差数列的前19项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
抛掷三枚质地均匀硬币,至少一次正面朝上的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
一个算法的程序框图如图所示,若该程度输出的结果为
,则判断框①中应填入的条件是( )

| 7 |
| 12 |

| A、i<5 | B、i<4 |
| C、i>4 | D、i≤3 |
已知A={x|x2-4x+3≤0},B={x|x2+mx+n<0},且A∩B≠∅,A∪B={x|1≤x<4},则m2-
n的取值范围为( )
| 5 |
| 2 |
| A、[15,19] |
| B、[14,18] |
| C、[15,19) |
| D、[14,18) |
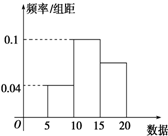 如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别为( )
如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数分别为( )| A、10 13 |
| B、12.5 12 |
| C、12.5 13 |
| D、10 15 |
已知函数f(x)=x3+ax2+6x-9有两个极值点x1,x2,且x12+x22=5,则a=( )
A、
| ||
B、-
| ||
C、±
| ||
| D、2 |
已知函数f(x)的图象向右平移1个单位长度后关于y轴对称,当x2>x1>-1时,
>0恒成立,设a=f(-2),b=f(-
),c=f(3),则a,b,c的大小关系为( )
| f(x2)-f(x1) |
| x2-x1 |
| 1 |
| 2 |
| A、c>a>b |
| B、c>b>a |
| C、a>c>b |
| D、b>a>c |
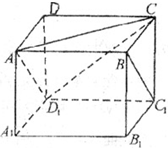 如图,正方体ABCD-A1B1C1D1,则下列四个命题:
如图,正方体ABCD-A1B1C1D1,则下列四个命题: