题目内容
直线（m+2）x+（2-m）y=2m在x轴上的截距为3，则m的值是（ ）
A、
| ||
B、-
| ||
| C、6 | ||
| D、-6 |
考点：直线的一般式方程
专题：直线与圆
分析：利用直线的截距的意义即可得出．
解答：
解：∵直线（m+2）x+（2-m）y=2m在x轴上的截距为3，
∴直线过（3，0），
代入可得3（m+2）=2m，解得m=-6．
故选：D．
∴直线过（3，0），
代入可得3（m+2）=2m，解得m=-6．
故选：D．
点评：本题考查了直线的截距的意义，属于基础题．
练习册系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
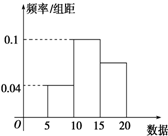如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数分别为（ ）| A、10 13 |
| B、12.5 12 |
| C、12.5 13 |
| D、10 15 |
已知函数f（x）是R上的偶函数，且在（0，+∞）上单调递减，则f（a2-2a+3）与f（-2）的大小关系为（ ）
| A、f（a2-2a+3）＞f（-2） |
| B、f（a2-2a+3）＜f（-2） |
| C、f（a2-2a+3）≥f（-2） |
| D、f（a2-2a+3）≤f（-2） |
设函数f（x）=
，若f（a）＜-1，则实数a的取值范围是（ ）
|
| A、（-∞，-1） |
| B、（-∞，-1）∪[0，2） |
| C、（2，+∞） |
| D、（-∞，-1）∪（2，+∞） |
已知函数f（x）的图象向右平移1个单位长度后关于y轴对称，当x2＞x1＞-1时，
＞0恒成立，设a=f（-2），b=f（-
），c=f（3），则a，b，c的大小关系为（ ）
| f(x2)-f(x1) |
| x2-x1 |
| 1 |
| 2 |
| A、c＞a＞b |
| B、c＞b＞a |
| C、a＞c＞b |
| D、b＞a＞c |
直线y=x+a与圆x2+y2=4交于点A、B，若
•
=-2（O为坐标原点），则实数a的为（ ）
| OA |
| OB |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
已知函数f（x）=sinx，下面结论错误的是（ ）
| A、f（x）的最小正周期是2π | ||||||||
B、f（x）在[0，
| ||||||||
C、f（x）[
| ||||||||
| D、f（x）的值域为[-1，1] |
在△ABC中，已知sin2B-sin2C-sin2A=sinAsinC，则角B的大小为（ ）
| A、150° | B、30° |
| C、120° | D、60° |