题目内容
已知tan
=2，求：
（1）tanα的值；
（2）
的值．
| α |
| 2 |
（1）tanα的值；
（2）
| 6sinα+cosα |
| 3sinα-2cosα |
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）原式利用二倍角的正切函数公式化简，将已知等式代入计算即可求出值；
（2）原式分子分母除以cosα，利用同角三角函数间基本关系化简，将tanα的值代入计算即可求出值．
（2）原式分子分母除以cosα，利用同角三角函数间基本关系化简，将tanα的值代入计算即可求出值．
解答：
解：（1）∵tan
=2，
∴tanα=
=
=-
；
（2）∵tanα=-
，
∴原式=
=
=
．
| α |
| 2 |
∴tanα=
2tan
| ||
1-tan2
|
| 2×2 |
| 1-22 |
| 4 |
| 3 |
（2）∵tanα=-
| 4 |
| 3 |
∴原式=
| 6tanα+1 |
| 3tanα-2 |
6×(-
| ||
3×(-
|
| 7 |
| 6 |
点评：此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
相关题目
已知集合A={x||x-2|＞2}，B={x|x∈N}，则（∁UA）∩B=（ ）
| A、{1，2，3} |
| B、{0，1，2，3} |
| C、{0，1，2，3，4} |
| D、{1，2，3，4} |
设f（x）是定义在R上的偶函数，且f（2+x）=f（2-x），当x∈[-2，0]时，f（x）=（
）x-1，若在区间（-2，6）内，函数y=f（x）-loga（x+2），（a＞0，a≠1）恰有1个零点，则实数a的取值范围是（ ）
| ||
| 2 |
| A、（1，4） | ||
| B、（4，+∞） | ||
C、（
| ||
| D、（0，1）∪（1，4） |
已知
=（2，1），
=（-1，k），如果
∥
，则实数k的值等于（ ）
| a |
| b |
| a |
| b |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
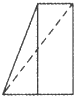
如图甲，将一个正三棱柱ABC-DEF截去一个三棱锥A-BCD，得到几何体BCDEF，如图乙，则该几何体的正视图（或称主视图）是（ ）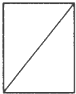
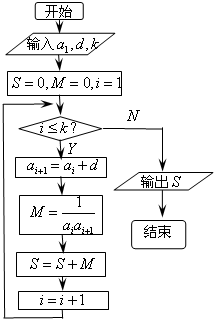已知数列{an}的各项均为正数，观察程序框图，当k=2时，S=