题目内容
9．
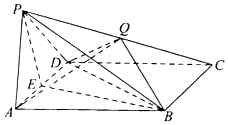已知四棱锥P-ABCD中，底面ABCD是菱形，PA=PD，∠BAD=60°，E是AD的中点，点Q在侧棱PC上．（I）求证：AD⊥平面PBE；
（II）若Q是PC的中点，求证PA∥平面BDQ．
分析 （Ⅰ）利用线面垂直的判定证明，关键是证明AD⊥PE，AD⊥BE；
（Ⅱ）连接AC交BD于点O，连接OQ，证明OQ∥PA，即可得到结论．
解答 证明：（Ⅰ）由E是AD的中点，PA=PD，所以AD⊥PE…（2分）
又底面ABCD是菱形，∠BAD=60°，
所以AB=BD，又因为E是AD的中点，
所以AD⊥BE…（4分）
又PE∩BE=E…（5分）
所以AD⊥平面PBE…（6分）
（Ⅱ）连接AC交BD于点O，连接OQ…（7分）
因为O是AC的中点，Q是PC的中点，所以OQ∥PA…（9分）
又PA?平面BDQ…（10分）
OQ?平面BDQ…（11分）
所以PA∥平面BDQ…（12分）
点评 本题考查线面垂直，考查线面平行，解题的关键是掌握线面垂直、线面平行的判定，属于中档题．
练习册系列答案
相关题目
19．已知f（x）=$\left\{\begin{array}{l}{2x+3，x＜0}\\{2{x}^{2}+1，x≥0}\end{array}\right.$，则f[f（-1）]的值是（ ）
| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
20．已知tan（α+$\frac{π}{4}$）=$\frac{1}{2}$，且α∈（-$\frac{π}{2}$，0），则$\frac{{2{{sin}^2}α+sin2α}}{{cos（α-\frac{π}{4}）}}$=（ ）
| A． | $-\frac{{3\sqrt{5}}}{10}$ | B． | $-\frac{{2\sqrt{5}}}{5}$ | C． | $\frac{{2\sqrt{5}}}{5}$ | D． | $\frac{{3\sqrt{10}}}{10}$ |
18．已知函数f（x）=cos（ωx+φ）（ω＞0）图象的两条相邻对称轴之间距离是$\frac{π}{2}$，若f（x）≤f（$-\frac{7π}{8}$），则函数y=sin（ωx+φ）一个单调递增区间是（ ）
| A． | $[-\frac{3π}{8}，\frac{π}{8}]$ | B． | $[\frac{π}{8}，\frac{5π}{8}]$ | C． | $[-\frac{5π}{8}，-\frac{π}{8}]$ | D． | $[-\frac{π}{8}，\frac{3π}{8}]$ |