题目内容
已知直线l1的方程为x-
y+1=0,其倾斜角为α.过点P(-
,2)的直线l的倾斜角为β,且β=2α.
(1)求直线l的一般式方程;
(2)
的值.
| 2 |
| 2 |
(1)求直线l的一般式方程;
(2)
| cos2β |
| 1+cos2β-sin2β |
考点:同角三角函数基本关系的运用,直线的点斜式方程
专题:三角函数的求值
分析:(1)由直线斜率与倾斜角的关系,根据直线l1的方程求出tanα的值,再由β=2α,利用二倍角的正切函数公式求出tanβ的值,确定出直线l斜率,进而确定出直线l方程;
(2)原式利用二倍角的正弦、余弦函数公式化简,整理后利用同角三角函数间基本关系化简,将tanβ的值代入计算即可求出值.
(2)原式利用二倍角的正弦、余弦函数公式化简,整理后利用同角三角函数间基本关系化简,将tanβ的值代入计算即可求出值.
解答:
解:(1)由l1的方程得tanα=
,
又β=2α,∴tanβ=
=
=2
,
∴直线l的斜率k=tanβ=2
,
由点斜式得l的方程为:y-2=2
(x+
),
化为一般方程:2
x-y+6=0;
(2)∵tanβ=2
,
∴
=
=
=
=
=
=
+
.
| ||
| 2 |
又β=2α,∴tanβ=
| 2tanα |
| 1-tan2α |
2×
| ||||
1-(
|
| 2 |
∴直线l的斜率k=tanβ=2
| 2 |
由点斜式得l的方程为:y-2=2
| 2 |
| 2 |
化为一般方程:2
| 2 |
(2)∵tanβ=2
| 2 |
∴
| cos2β |
| 1+cos2β-sin2β |
| cos2β-sin2β |
| 2cos2β-2sinβcosβ |
| (cosβ+sinβ)(cosβ-sinβ) |
| 2cosβ(cosβ-sinβ) |
| cosβ+sinβ |
| 2cosβ |
| 1+tanβ |
| 2 |
1+2
| ||
| 2 |
| 1 |
| 2 |
| 2 |
点评:此题考查了同角三角函数基本关系的运用,以及直线的点斜式方程,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
已知
=(1,1,0)与
=(-1,0,2),且k
+
与2
-
互相垂直,则k=( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
| C、-2 | ||
D、
|
从伦敦奥运会的一张贵宾票和两张普通票中随机抽取一张,抽到贵宾票的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
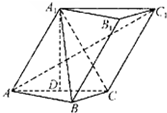 已知三棱柱ABC-A1B1C1中,∠BCA=90°,AA1=AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.
已知三棱柱ABC-A1B1C1中,∠BCA=90°,AA1=AC=BC=2,A1在底面ABC上的射影恰为AC的中点D.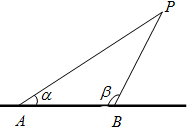 根据国际公法,外国船只不得进入离我国海岸线12海里以内的区域(此为我国领海,含分界线).若外国船只进入我国领海,我方将向其发出警告令其退出.如图,已知直线AB为海岸线,A,B是相距12海里的两个观测站,现发现一外国船只航行于点P处,此时我方测得∠BAP=α,∠ABP=β(0<α<π,0<β<π).
根据国际公法,外国船只不得进入离我国海岸线12海里以内的区域(此为我国领海,含分界线).若外国船只进入我国领海,我方将向其发出警告令其退出.如图,已知直线AB为海岸线,A,B是相距12海里的两个观测站,现发现一外国船只航行于点P处,此时我方测得∠BAP=α,∠ABP=β(0<α<π,0<β<π).