题目内容
设函数f(x)=x3-6x+5,x∈R
(1)求f(x)的单调区间和极值;
(2)若直线y=a与y=f(x)的图象有三个不同的交点,求实数a的取值范围;
(3)已知当x∈(1,+∞)时,f(x)≥k(x-1)恒成立,求实数k的取值范围.
(1)求f(x)的单调区间和极值;
(2)若直线y=a与y=f(x)的图象有三个不同的交点,求实数a的取值范围;
(3)已知当x∈(1,+∞)时,f(x)≥k(x-1)恒成立,求实数k的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性,利用导数研究函数的极值
专题:综合题,导数的综合应用
分析:(1)求导数,令f′(x)=0可得极值点,解不等式f′(x)>0,f′(x)<0可得单调区间;根据导数符号变化情况可判断极值并可求解;
(2)由(1)作出函数的草图,由图象可得a的范围;
(3)x∈(1,+∞)时,f(x)≥k(x-1)可化为x2+x-5≥k,令g(x)=x2+x-5,由二次函数的性质可求g(x)的最小值,从而可得k的范围;
(2)由(1)作出函数的草图,由图象可得a的范围;
(3)x∈(1,+∞)时,f(x)≥k(x-1)可化为x2+x-5≥k,令g(x)=x2+x-5,由二次函数的性质可求g(x)的最小值,从而可得k的范围;
解答:
 解:(1)f′(x)=3(x2-2),令f′(x)=0,得x1=-
解:(1)f′(x)=3(x2-2),令f′(x)=0,得x1=-
,x2=
,
∴当x<-
或x>
时,f′(x)>0;当-
<x<
时,f′(x)<0,
∴f(x)的单调递增区间是(-∞,-
)和(
,+∞),单调递减区间是(-
,
);
当x=-
,f(x)有极大值5+4
;当x=
,f(x)有极小值5-4
.
(2)由(1)可知y=f(x)图象的大致形状及走向如图所示:
∴当5-4
<a<5+4
时,直线y=a与y=f(x)的图象有3个不同交点;
(3)f(x)≥k(x-1)即(x-1)(x2+x-5)≥k(x-1),
∵x∈(1,+∞)上恒成立,∴x2+x-5≥k,
令g(x)=x2+x-5,由二次函数的性质,g(x)在(1,+∞)上是增函数,
∴g(x)>g(1)=-3,
∴所求k的取值范围是k≤-3.
 解:(1)f′(x)=3(x2-2),令f′(x)=0,得x1=-
解:(1)f′(x)=3(x2-2),令f′(x)=0,得x1=-| 2 |
| 2 |
∴当x<-
| 2 |
| 2 |
| 2 |
| 2 |
∴f(x)的单调递增区间是(-∞,-
| 2 |
| 2 |
| 2 |
| 2 |
当x=-
| 2 |
| 2 |
| 2 |
| 2 |
(2)由(1)可知y=f(x)图象的大致形状及走向如图所示:
∴当5-4
| 2 |
| 2 |
(3)f(x)≥k(x-1)即(x-1)(x2+x-5)≥k(x-1),
∵x∈(1,+∞)上恒成立,∴x2+x-5≥k,
令g(x)=x2+x-5,由二次函数的性质,g(x)在(1,+∞)上是增函数,
∴g(x)>g(1)=-3,
∴所求k的取值范围是k≤-3.
点评:该题考查利用导数研究函数的单调性、极值、最值,考查函数恒成立,考查数形结合思想,考查学生解决问题的能力,恒成立问题常转化为函数最值解决.

练习册系列答案
相关题目
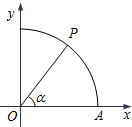 如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.
如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α. 在平面直角坐标系xOy中,已知圆C经过A(2,-2),B(1,1)两点,且圆心在直线x-2y-2=0上.
在平面直角坐标系xOy中,已知圆C经过A(2,-2),B(1,1)两点,且圆心在直线x-2y-2=0上.