题目内容
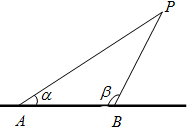 根据国际公法,外国船只不得进入离我国海岸线12海里以内的区域(此为我国领海,含分界线).若外国船只进入我国领海,我方将向其发出警告令其退出.如图,已知直线AB为海岸线,A,B是相距12海里的两个观测站,现发现一外国船只航行于点P处,此时我方测得∠BAP=α,∠ABP=β(0<α<π,0<β<π).
根据国际公法,外国船只不得进入离我国海岸线12海里以内的区域(此为我国领海,含分界线).若外国船只进入我国领海,我方将向其发出警告令其退出.如图,已知直线AB为海岸线,A,B是相距12海里的两个观测站,现发现一外国船只航行于点P处,此时我方测得∠BAP=α,∠ABP=β(0<α<π,0<β<π).(1)试问当α=30°,β=120°时,我方是否应向该外国船只发出警告?
(2)若tanα=
| 1 |
| 2 |
考点:解三角形的实际应用
专题:解三角形
分析:(1)过P作PH垂直AB于H,先根据已知求得∠APB,进而求得AB,进而表示出PH与12进行比较.
(2)先由正弦定理求得PB的表达式,进而取得PH的表达式,令PH≤12,求得β的范围.
(2)先由正弦定理求得PB的表达式,进而取得PH的表达式,令PH≤12,求得β的范围.
解答:
解:(1)如图:过P作PH垂直AB于H,因为α=30°,β=120°,
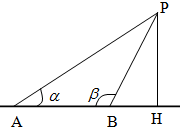
所以∠APB=30°,所以AB=PB=12,
所以PH=ABsin60°=6
<12,
所以应向该外国船只发出警告.
(2)在△ABP中,由正弦定理得:
=
,
所以PB=
,
所以PH=PB•sin(π-β)=
=
,
令PH≤12,得
≤12,即sinαsinβ≤sin(α+β),
所以sinαsinβ≤sinαcosβ+cosαsinβ,
又因为tanα=
,所以α为锐角,且sinα=
,cosα=
,
所以
sinβ≤
cosβ+
sinβ,即sinβ≥-cosβ,
故sinβ+cosβ≥0,即
sin(β+
)≥0,解得0<β≤
,
所以当0<β≤
时,我方应向该外国船只发出警告.

所以∠APB=30°,所以AB=PB=12,
所以PH=ABsin60°=6
| 3 |
所以应向该外国船只发出警告.
(2)在△ABP中,由正弦定理得:
| AB |
| sin(π-α-β) |
| PB |
| sinα |
所以PB=
| 12sinα |
| sin(π-α-β) |
所以PH=PB•sin(π-β)=
| 12sinαsinβ |
| sin(π-α-β) |
| 12sinαsinβ |
| sin(α+β) |
令PH≤12,得
| 12sinαsinβ |
| sin(α+β) |
所以sinαsinβ≤sinαcosβ+cosαsinβ,
又因为tanα=
| 1 |
| 2 |
| ||
| 5 |
2
| ||
| 5 |
所以
| ||
| 5 |
| ||
| 5 |
2
| ||
| 5 |
故sinβ+cosβ≥0,即
| 2 |
| π |
| 4 |
| 3π |
| 4 |
所以当0<β≤
| 3π |
| 4 |
点评:本题主要考查了解三角形问题的实际应用.解题的关键时把文字描述语言转化成数学模型.

练习册系列答案
相关题目
函数f(x)=
+lg(3x-1)的定义域是( )
| x2-1 | ||
|
| A、(-∞,-1) | ||
B、(-1,
| ||
C、(-
| ||
D、(
|
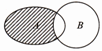
已知全集U=R,集合A={0,1,2,3,4,5},B=[2,+∞),则图中阴影部分所表示的集合( )

| A、{1} |
| B、{0,1} |
| C、{1,2} |
| D、{0,1,2} |
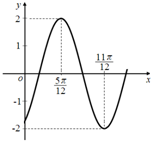 已知函数f(x)=Asin(ωx-
已知函数f(x)=Asin(ωx- 在平面直角坐标系xOy中,已知圆C经过A(2,-2),B(1,1)两点,且圆心在直线x-2y-2=0上.
在平面直角坐标系xOy中,已知圆C经过A(2,-2),B(1,1)两点,且圆心在直线x-2y-2=0上.