题目内容
已知sin(π-α)=
,α∈(
,π).
(1)求cos(π+α)的值;
(2)求tan(π-α)的值;
(3)求sin2α+cos2α的值.
| 3 |
| 5 |
| π |
| 2 |
(1)求cos(π+α)的值;
(2)求tan(π-α)的值;
(3)求sin2α+cos2α的值.
考点:运用诱导公式化简求值,二倍角的正弦,二倍角的余弦
专题:分割补形法
分析:利用诱导公式以及同角三角函数的基本关系式,直接求解(1)(2),利用二倍角公式化简求解(3)即可.
解答:
(本小题满分12分)
解:(1)∵sin(π-α)=
,∴sinα=
(1分)
又α∈(
,π),∴cosα=-
=-
=-
(3分)
∴cos(π+α)=-cosα=
(4分)
(2)∵tanα=
=
=-
(6分)
∴tan(π-α)=-tanα=
(7分)
(3)∵sinα=
,cosα=-
∴sin2α=2sinαcosα=2×
×(-
)=-
(9分)cos2α=2cos2α-1=2×(-
)2-1=
(11分)
∴sin2α+cos2α=-
+
=-
(12分)
解:(1)∵sin(π-α)=
| 3 |
| 5 |
| 3 |
| 5 |
又α∈(
| π |
| 2 |
| 1-sin2α |
1-(
|
| 4 |
| 5 |
∴cos(π+α)=-cosα=
| 4 |
| 5 |
(2)∵tanα=
| sinα |
| cosα |
| ||
-
|
| 3 |
| 4 |
∴tan(π-α)=-tanα=
| 3 |
| 4 |
(3)∵sinα=
| 3 |
| 5 |
| 4 |
| 5 |
∴sin2α=2sinαcosα=2×
| 3 |
| 5 |
| 4 |
| 5 |
| 24 |
| 25 |
| 4 |
| 5 |
| 7 |
| 25 |
∴sin2α+cos2α=-
| 24 |
| 25 |
| 7 |
| 25 |
| 17 |
| 25 |
点评:不考查诱导公式的应用,同角三角函数的基本关系式的应用以及二倍角公式的应用,基本知识的考查.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
已知
=(cosα,sinα),
=(1,-1),α∈[-
,0],则
与
夹角的取值范围为( )
| OA |
| OB |
| π |
| 2 |
| OA |
| OB |
A、(0,
| ||||
B、(
| ||||
C、[0,
| ||||
D、[
|
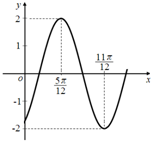 已知函数f(x)=Asin(ωx-
已知函数f(x)=Asin(ωx-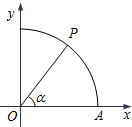 如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.
如图,曲线Γ:x2+y2=1(x≥0,y≥0)与x轴交于点A,点P在曲线Γ上,∠AOP=α.