题目内容
11.已知函数f(x)=Asin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则下列判断正确的是( )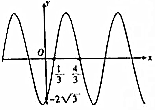
| A. | 函数f(x)的最小正周期为π | |
| B. | 函数f(x)的值域为[-$\frac{7}{2}$,$\frac{7}{2}$] | |
| C. | 函数f(x)的图象关于直线x=-$\frac{1}{6}$对称 | |
| D. | 函数f(x)的图象向右平移$\frac{1}{3}$个单位得到函数y=Asinωx的图象 |
分析 由周期求出ω,由五点法作图求出φ的值,可得f(x)的解析式;再利用函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象和性质,得出结论.
解答 解:根据函数f(x)=Asin(ωx+φ)(ω>0,-π<φ<0)的部分图象,可得$\frac{T}{2}$=$\frac{π}{ω}$=$\frac{4}{3}$-$\frac{1}{3}$,∴ω=π.
再根据五点法作图可得π•$\frac{1}{3}$+φ=0,∴φ=-$\frac{π}{3}$,即f(x)=Asin(πx-$\frac{π}{3}$),
故函数的周期为$\frac{2π}{π}$=2,故排除A;由于A不确定,故函数f(x)的值域不确定,故排除B;
令x=-$\frac{1}{6}$,可得f(x)=-A,为函数的最小值,故函数f(x)的图象关于直线x=-$\frac{1}{6}$对称,故C正确;
把函数f(x)的图象向右平移$\frac{1}{3}$个单位得到函数y=Asin[π(x-$\frac{1}{3}$)-$\frac{π}{3}$]=Asin(πx-$\frac{2π}{3}$)的图象,故D错误,
故选:C.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由周期求出ω,由五点法作图求出φ的值;函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
19.双曲线$\frac{x^2}{4}-\frac{y^2}{12}=1$的焦点到渐近线的距离为( )
| A. | $2\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
6.下列函数,是偶函数,且周期为π的是( )
| A. | y=cos2x-sin2x | B. | y=sin2x+cos2x | C. | y=cos2x-sin2x | D. | y=sin2x+cosx |
16.在三棱锥P-ABC中,PA⊥平面ABC,PA=2$\sqrt{3}$,BC=2,则三棱锥P-ABC的外接球的表面积的最小值为( )
| A. | 13π | B. | 14π | C. | 15π | D. | 16π |
3.“a=-1”是“直线ax+3y+2=0与直线x+(a-2)y+1=0平行”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.若a>0,且a≠1,则“函数y=ax在R上是减函数”是“函数y=(2-a)x3在R上是增函数”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.阅读如图所示的程序框图,运行相应程序,输出的结果是( )


| A. | 242 | B. | 274 | C. | 275 | D. | 338 |
 若某市6所中学参加中学生合唱比赛的得分用茎叶图表示如图,其中茎为十位数,叶为个位数,则这组数据的方差是$\frac{13}{3}$.
若某市6所中学参加中学生合唱比赛的得分用茎叶图表示如图,其中茎为十位数,叶为个位数,则这组数据的方差是$\frac{13}{3}$.