题目内容
11.已知直线l经过点P(1,0)且与以A(2,1),B(3,-2)为端点的线段AB有公共点,则直线l的倾斜角的取值范围是[0,45°]∪[135°,180°).分析 利用斜率计算公式、三角函数的单调性即可得出.
解答  解:∵kPA=$\frac{1-0}{2-1}$=1,kPB=$\frac{-2-0}{3-1}$=-1.
解:∵kPA=$\frac{1-0}{2-1}$=1,kPB=$\frac{-2-0}{3-1}$=-1.
∴直线PA,PB的倾斜角分别为45°,135°.
∵直线l与连接A(2,1),B(3,-2)的线段有公共点,
∴直线l的斜率k满足-1≤k≤1
∴直线l的倾斜角的取值范围是[0,45°]∪[135°,180°).
故答案为:[0,45°]∪[135°,180°).
点评 本题考查了斜率计算公式、三角函数的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.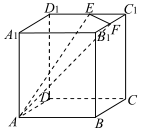 如图所示,在棱长为 6的正方体ABCD-A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,过A,E,F三点作该正方体的截面,则截面的周长为( )
如图所示,在棱长为 6的正方体ABCD-A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,过A,E,F三点作该正方体的截面,则截面的周长为( )
 如图所示,在棱长为 6的正方体ABCD-A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,过A,E,F三点作该正方体的截面,则截面的周长为( )
如图所示,在棱长为 6的正方体ABCD-A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,过A,E,F三点作该正方体的截面,则截面的周长为( )| A. | $18+3\sqrt{2}$ | B. | $6\sqrt{13}+3\sqrt{2}$ | C. | $6\sqrt{5}+9\sqrt{2}$ | D. | $10+3\sqrt{2}+4\sqrt{10}$ |
16.在钝角△ABC中,a、b、c分别为角A、B、C的对边,已知面积S=$\frac{1}{2},AB=1,BC=\sqrt{2}$,则AC=( )
| A. | 5 | B. | $\sqrt{5}$ | C. | 2 | D. | 1 |
3.一条直线和该直线外不共线的三点最多可以确定平面的个数为( )
| A. | 1个 | B. | 3个 | C. | 4个 | D. | 6个 |