题目内容
19.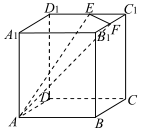 如图所示,在棱长为 6的正方体ABCD-A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,过A,E,F三点作该正方体的截面,则截面的周长为( )
如图所示,在棱长为 6的正方体ABCD-A1B1C1D1中,点E,F分别是棱C1D1,B1C1的中点,过A,E,F三点作该正方体的截面,则截面的周长为( )| A. | $18+3\sqrt{2}$ | B. | $6\sqrt{13}+3\sqrt{2}$ | C. | $6\sqrt{5}+9\sqrt{2}$ | D. | $10+3\sqrt{2}+4\sqrt{10}$ |
分析 由题意画出截面五边形,再由已知利用勾股定理求得边长得答案.
解答 解:如图,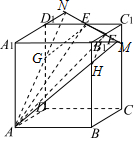
延长EF、A1B1 相交于M,连接AM交BB1 于H,
延长FE、A1D1 相交于N,连接AN交DD1 于G,
可得截面五边形AHFEG.
∵ABCD-A1B1C1D1是边长为6的正方体,且E,F分别是棱C1D1,B1C1的中点,
∴EF=3$\sqrt{2}$,AG=AH=$\sqrt{{6}^{2}+{4}^{2}}=2\sqrt{13}$,EG=FH=$\sqrt{{3}^{2}+{2}^{2}}=\sqrt{13}$.
∴截面的周长为$6\sqrt{13}+3\sqrt{2}$.
故选:B.
点评 本题考查棱柱的结构特征,考查空间想象能力和思维能力,是中档题.

练习册系列答案
相关题目
7.一个几何体的三视图如图所示,则该几何体的体积为( )
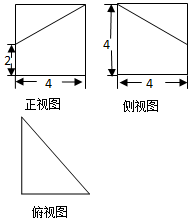

| A. | $\frac{32}{3}$ | B. | $\frac{50}{3}$ | C. | $\frac{64}{3}$ | D. | $\frac{80}{3}$ |