题目内容
若直线y=t与函数y=x3-3x的图象有三个公共点，求实数t的取值范围．
考点：根的存在性及根的个数判断
专题：函数的性质及应用,导数的综合应用
分析：利用导数研究函数y=x3-3x的图象与性质，求出函数在极大值与极小值，画出函数的图象，根据图象求出t的取值范围．
解答：
解：∵y=x3-3x，
∴y'=3x2-3=3（x+1）（x-1），…（2分）
∴当x∈（-∞，-1）或x∈（1，+∞）时，
y'＞0，y=x3-3x为增函数；
当x∈（-1，1）时，
y'＜0，y=x3-3x为减函数；…（4分）
∴当x=1时，y=x3-3x有极小值是13-3×1=-2；
当x=-1时，y=x3-3x有极大值是（-1）3-3×（-1）=2；…（6分）
画出图象，如图所示；
由题意，结合图象得-2＜t＜2．…（10分）
∴y'=3x2-3=3（x+1）（x-1），…（2分）
∴当x∈（-∞，-1）或x∈（1，+∞）时，
y'＞0，y=x3-3x为增函数；
当x∈（-1，1）时，
y'＜0，y=x3-3x为减函数；…（4分）
∴当x=1时，y=x3-3x有极小值是13-3×1=-2；
当x=-1时，y=x3-3x有极大值是（-1）3-3×（-1）=2；…（6分）
画出图象，如图所示；
由题意，结合图象得-2＜t＜2．…（10分）
点评：本题考查了利用导数研究函数的图象与性质的问题，解题时应画出函数的图象，结合图象解答问题，是中档题目．
练习册系列答案
相关题目
函数y=
（a＞1）的图象的大致形状是（ ）
| |x| |
| xax |
A、 |
B、 |
C、 |
D、 |
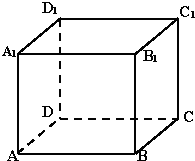在正方体ABCD-A1B1C1D1中，棱长为a，M、N分别是A1B和AC的中点．