题目内容
14.已知函数f(n)=k,(n∈N*),k是$\sqrt{2}$小数点后第n位数字,$\sqrt{2}$=1.414213562…,则$\underbrace{f\{f…f[{f(8)}]\}}_{2016个f}$=( )| A. | 1 | B. | 2 | C. | 4 | D. | 6 |
分析 利用递推思想求出f(8)=6,f(f(8))=f(6)=3,f(f(f(8)))=f(3)=4,f(f(f(f(8))))=f(4)=2,f(f(f(f(f(8)))))=f(2)=1,f(f(f(f(f(f(8))))))=f(1)=4,再利用函数的周期性质能求出结果.
解答 解:∵函数f(n)=k,(n∈N*),k是$\sqrt{2}$小数点后第n位数字,$\sqrt{2}$=1.414213562…,
∴f(8)=6,
f(f(8))=f(6)=3,
f(f(f(8)))=f(3)=4,
f(f(f(f(8))))=f(4)=2,
f(f(f(f(f(8)))))=f(2)=1,
f(f(f(f(f(f(8))))))=f(1)=4,
∴$\underbrace{f\{f…f[{f(8)}]\}}_{2016个f}$=f(1)=4.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
17.设全集U=R,集合A={x|x2-2x-3<0},B={x|x-1≥0},则图中阴影部分所表示的集合为( )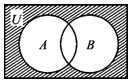

| A. | {x|x≤-1或x≥3} | B. | {x|x<1或x≥3} | C. | {x|x≤1} | D. | {x|x≤-1} |
18.某三棱锥的三视图如图所示,则该三棱锥中最长棱的长度为( )
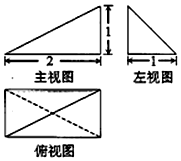

| A. | $\sqrt{5}$ | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | 3 |