题目内容
2.已知函数y=f(x)是R上的偶函数,设a=ln$\frac{1}{π}$,b=(lnπ)2,c=ln$\sqrt{π}$,当任意x1、x2∈(0,+∞)时,都有(x1-x2)•[f(x1)-f(x2)]<0,则( )| A. | f(a)>f(b)>f(c) | B. | f(b)>f(a)>f(c) | C. | f(c)>f(b)>f(a) | D. | f(c)>f(a)>f(b) |
分析 根据减函数的定义便可看出f(x)在(0,+∞)上单调递减,根据f(x)为偶函数可以得到f(a)=f(lnπ),而$f(c)=f(\frac{1}{2}lnπ)$,可以比较$lnπ,\frac{1}{2}lnπ$和(lnπ)2的大小,根据减函数的定义即可得出f(a),f(b),f(c)的大小关系,从而找出正确选项.
解答 解:依题意函数y=f(x)在(0,+∞)上为减函数;
∵f(x)是R上的偶函数;
∴f(a)=f(-a)=$f(-ln\frac{1}{π})=f(lnπ)$,$f(c)=f(ln\sqrt{π})=f(\frac{1}{2}lnπ)$;
∵$0<\frac{1}{2}lnπ<lnπ<(lnπ)^{2}$;
∴$f(\frac{1}{2}lnπ)>f(lnπ)>f((lnπ)^{2})$;
即f(c)>f(a)>f(b).
故选:D.
点评 考查偶函数的定义,减函数的定义,以及根据减函数的定义判断一个函数为减函数的方法,对数的运算性质.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
7.若x,y满足不等式组$\left\{\begin{array}{l}{2x-3y-6≥0}\\{x+y-3≥0}\\{x≤a}\end{array}\right.$,z=x-y的最大值为4,则实数a=( )
| A. | 4 | B. | $\frac{7}{2}$ | C. | 5 | D. | $\frac{9}{2}$ |
14.设命题p:?x∈(0,+∞),$\sqrt{x}$≥log2x,则¬p为( )
| A. | ?x∈(0,+∞),$\sqrt{x}$≥log2x | B. | ?x∈(0,+∞),$\sqrt{x}$<log2x | C. | ?x∈(0,+∞),$\sqrt{x}$=log2x | D. | ?x∈(0,+∞),$\sqrt{x}$<log2x |
11.已知圆(x-2)2+(y+1)2=16的一条直径恰好经过直线x-2y-3=0被圆所截弦的中点,则该直径所在直线的方程为( )
| A. | x-2y=0 | B. | 2x+y-5=0 | C. | 2x+y-3=0 | D. | x-2y+4=0 |
12.阅读如图所示的程序框图,运行相应的程序,输出的结果s=( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
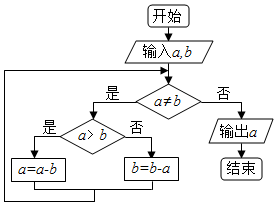 上边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为15,18,则输出的a为( )
上边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a,b分别为15,18,则输出的a为( )