题目内容
13.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=2,且|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=2,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角等于$\frac{2π}{3}$.分析 求出$\overrightarrow{a}•\overrightarrow{b}$,代入向量夹角公式计算.
解答 解:∵$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}-\overrightarrow{a}•\overrightarrow{b}$=2,
∴$\overrightarrow{a}•\overrightarrow{b}$=-1.
∴cos<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=-$\frac{1}{2}$.
∴<$\overrightarrow{a},\overrightarrow{b}$>=$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
相关题目
4.函数f(x)的定义域为[-1,1],图象如图1所示:函数g(x)的定义域为[-2,2],图象如图2所示,方程f(g(x))=0有m个实数根,方程g(f(x))=0有n个实数根,则m+n=( )
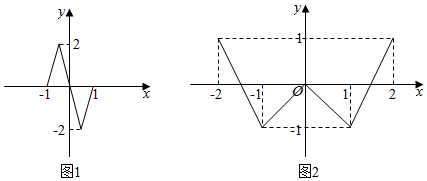

| A. | 14 | B. | 12 | C. | 10 | D. | 8 |
18.微信是腾讯公司推出的一种手机通讯软件,它支持发送语音短信、视频、图片和文字,经推出便风靡全国,甚至涌现出一批在微信的朋友圈销售商的人(简称微商),为了调查每天微信用户使用微信的时间,某经销化妆品的微商在一广场随机采访男性、女性用户各50名,其中每天玩微信超过4小时的用户为“微信控”,否则称其为“非微信控”,调查结果如下:
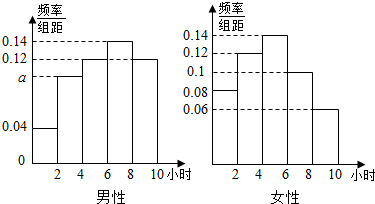
(1)根据以上数据,能否有60%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“微信控”与“非微信控”的人数;
(3)从(2)中抽取的5人中在随机抽取2人赠送200元的护肤品套装,求这2人至少有1人为“非微信控”的概率.
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
参数数据:

(1)根据以上数据,能否有60%的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份,求所抽取5人中“微信控”与“非微信控”的人数;
(3)从(2)中抽取的5人中在随机抽取2人赠送200元的护肤品套装,求这2人至少有1人为“非微信控”的概率.
参考公式:${K^2}=\frac{{n{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d.
参数数据:
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| k0 | 0.455 | 0.708 | 1.321 | 3.840 | 5.024 | 6.635 |
2.已知函数y=f(x)是R上的偶函数,设a=ln$\frac{1}{π}$,b=(lnπ)2,c=ln$\sqrt{π}$,当任意x1、x2∈(0,+∞)时,都有(x1-x2)•[f(x1)-f(x2)]<0,则( )
| A. | f(a)>f(b)>f(c) | B. | f(b)>f(a)>f(c) | C. | f(c)>f(b)>f(a) | D. | f(c)>f(a)>f(b) |
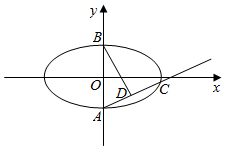 如图,在平面直角坐标系xOy中,椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{6}}{3}$,过椭圆右焦点且垂直于x轴的直线交椭圆所得的弦的弦长为$\frac{2\sqrt{3}}{3}$,过点A的直线与椭圆W交于另一点C,
如图,在平面直角坐标系xOy中,椭圆W:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{6}}{3}$,过椭圆右焦点且垂直于x轴的直线交椭圆所得的弦的弦长为$\frac{2\sqrt{3}}{3}$,过点A的直线与椭圆W交于另一点C,