题目内容
14．设命题p：?x∈（0，+∞），$\sqrt{x}$≥log2x，则￢p为（ ）| A． | ?x∈（0，+∞），$\sqrt{x}$≥log2x | B． | ?x∈（0，+∞），$\sqrt{x}$＜log2x | C． | ?x∈（0，+∞），$\sqrt{x}$=log2x | D． | ?x∈（0，+∞），$\sqrt{x}$＜log2x |
分析 利用特称命题的否定是全称命题写出结果即可．
解答 解：因为特称命题的否定是全称命题，所以，命题p：?x∈（0，+∞），$\sqrt{x}$≥log2x，则￢p为：?x∈（0，+∞），$\sqrt{x}$＜log2x．
故选：B．
点评 本题考查命题的否定，特称命题与全称命题的否定关系，是基础题．
练习册系列答案
新黄冈兵法密卷系列答案
相关题目
4．函数f（x）的定义域为[-1，1]，图象如图1所示：函数g（x）的定义域为[-2，2]，图象如图2所示，方程f（g（x））=0有m个实数根，方程g（f（x））=0有n个实数根，则m+n=（ ）
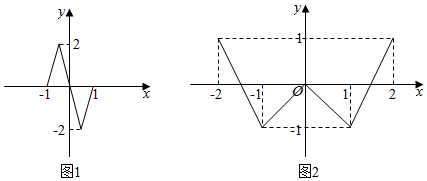
| A． | 14 | B． | 12 | C． | 10 | D． | 8 |
2．已知函数y=f（x）是R上的偶函数，设a=ln$\frac{1}{π}$，b=（lnπ）2，c=ln$\sqrt{π}$，当任意x1、x2∈（0，+∞）时，都有（x1-x2）•[f（x1）-f（x2）]＜0，则（ ）
| A． | f（a）＞f（b）＞f（c） | B． | f（b）＞f（a）＞f（c） | C． | f（c）＞f（b）＞f（a） | D． | f（c）＞f（a）＞f（b） |
19．阅读如图所示的程序框图，运行相应的程序，则输出的n的值为（ ）
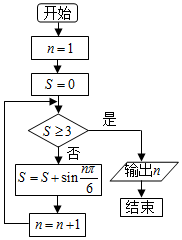
| A． | 3 | B． | 4 | C． | 5 | D． | 6 |
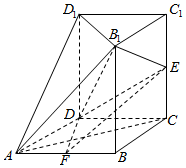如图，几何体ABCD-B1C1D1中，四边形ABCD为菱形，∠BAD=60°，AB=a，平面B1C1D1∥平面ABCD，BB1、CC1、DD1都垂直于平面ABCD，且BB1=$\sqrt{2}$a，E为CC1的中点，F为AB的中点．