题目内容
若sin(α-β)cosα-cos(α-β)sinα=
,且β∈(π,
π),则cos
为 .
| 4 |
| 5 |
| 3 |
| 2 |
| β |
| 2 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:由已知中sin(α-β)cosα-cos(α-β)sinα=
,且β∈(π,
π),利用诱导公式和差角正弦公式可得sinβ=-
,进而根据同角三角函数基本关系公式可得cosβ=-
,最后由半角公式得到答案.
| 4 |
| 5 |
| 3 |
| 2 |
| 4 |
| 5 |
| 3 |
| 5 |
解答:
解:∵sin(α-β)cosα-cos(α-β)sinα=sin(α-β-α)=sin(-β)=
,
∴sinβ=-
,
又∵β∈(π,
π),
∴
∈(
,
),且cosβ=-
=-
,
则cos
=-
=-
,
故答案为:-
| 4 |
| 5 |
∴sinβ=-
| 4 |
| 5 |
又∵β∈(π,
| 3 |
| 2 |
∴
| β |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 1-sin2β |
| 3 |
| 5 |
则cos
| β |
| 2 |
|
| ||
| 5 |
故答案为:-
| ||
| 5 |
点评:本题考查的知识点是诱导公式,差角正弦公式,同角三角函数基本关系公式和半角公式,综合性强,属于中档题.

练习册系列答案
相关题目
在△ABC中,若(
+
)•(
-
)=0,则△ABC为( )
| CA |
| CB |
| CA |
| CB |
| A、正三角形 | B、直角三角形 |
| C、等腰三角形 | D、无法确定 |
若?a∈(0,+∞),?θ∈R使asinθ≥a成立,则cos(θ-
)的值为( )
| π |
| 6 |
A、
| ||||
B、
| ||||
C、±
| ||||
D、±
|
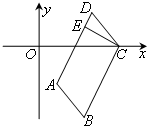 如图,在平行四边形ABCD中,边AD所在直线方程为2x-y-2=0,顶点C(2,0).
如图,在平行四边形ABCD中,边AD所在直线方程为2x-y-2=0,顶点C(2,0).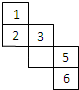 正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示.如图是一个正方体的表面展开图,若图中“4”在正方体的“前面”,则“后面”是( )
正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示.如图是一个正方体的表面展开图,若图中“4”在正方体的“前面”,则“后面”是( )