题目内容

在△ABC中，若（
CA
+
CB
 ）•（
CA
-
CB
）=0，则△ABC为（　　）
A、正三角形B、直角三角形
C、等腰三角形D、无法确定
考点：三角形的形状判断
专题：解三角形
分析：利用平面向量的数量积的运算性质可得（
CA
+
CB
 ）•（
CA
-
CB
）=
CA
2-
CB
2=b2-a2=0，从而可得答案．
解答： 解：∵在△ABC中，（
CA
+
CB
 ）•（
CA
-
CB
）=
CA
2-
CB
2=b2-a2=0，
∴a=b，
∴△ABC为等腰三角形，
故选：C．
点评：本题考查三角形形状的判断，考查向量的数量积的运算性质，属于中档题．
练习册系列答案
相关题目
⊙M：（x+1）2+y2=1及⊙N：（x-1）2+y2=9，动圆P与⊙M外切且与⊙N相内切，圆心P的轨迹为曲线C
①求曲线C的方程；
②Q为曲线C上任一点，求
QM
•
QN
的取值范围．
设数列{an}的前n项和为Sn，且满足Sn=n-an，n∈N*．
（1）求数列{an}的通项公式；
（2）设cn=-2nan+2n，数列{cn}的前n项和为Tn，求证：Tn＜4．
已知函数f（x）=-x3+3x2+9x+a．
（1）求f（x）的单调区间；
（2）若f（x）在区间[-2，2]上的最大值为20，求它在该区间上的最小值．
定义域为R的偶函数f（x）满足对?x∈R，有f（x+2）=f（x）+f（1），且当x∈[2，3]时，f（x）=-2x2+12x-18，若函数y=f（x）-loga（|x|+1）在（0，+∞）上至少有三个零点，则a的取值范围是（　　）
A、（0，
2
2
）
B、（0，
3
3
）
C、（0，
5
5
）
D、（0，
6
6
）
下列命题中，正确命题的个数为（　　）
①“若xy=0，则x=0或y=0”的逆否命题为“若x≠0且y≠0，则xy≠0；
②函数f（x）=ex+x-2的零点所在区间是（1，2）；
③x2-5x+6=0是x=2的必要不充分条件．
A、0B、1C、2D、3
直线L过A（1，1）与两坐标轴交于M、N两点，当L绕A旋转时，MN的中点轨迹方程为
 
．
若sin（α-β）cosα-cos（α-β）sinα=
4
5
，且β∈（π，
3
2
π），则cos 
β
2
为
 
．
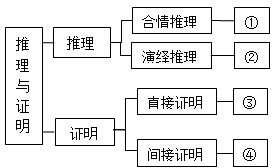如图是选修1-2第二章“推理与证明”的知识结构图（部分），如果要加入知识点“分析法”，则应该放在图（　　）
A、“①”处B、“②”处
C、“③”处D、“④”处

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网