题目内容

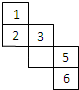正方体的六个面分别用“前面，后面，上面，下面，左面，右面”表示．如图是一个正方体的表面展开图，若图中“4”在正方体的“前面”，则“后面”是（　　）
A、1B、2C、5D、6
考点：表面展开图
专题：空间位置关系与距离
分析：由已知中正方体的表面展开图，可得2与5对面，3与6对面，故与4对面的数为1，进而得到答案．
解答： 解：在已知中正方体的表面展开图中，
2与5对面，3与6对面，故与4对面的数为1，
若图中“4”在正方体的“前面”，则“后面”是1，
故选：A
点评：本题考查了正方形相对两个面上的文字问题，同时考查空间想象能力．注意正方体的空间图形，从相对面入手，分析及解答问题．
练习册系列答案
相关题目
已知
a
=（1-cosx，sinx），
b
=（1+cosx，cosx）
（Ⅰ）若
a
•
b
=1，求x的值
（Ⅱ） 若f（x）=
a
•
b
+cosx（a-sinx）+1，x∈[
π
6
，
π
3
]且f（x）≤0恒成立，求a的取值范围？
定义域为R的偶函数f（x）满足对?x∈R，有f（x+2）=f（x）+f（1），且当x∈[2，3]时，f（x）=-2x2+12x-18，若函数y=f（x）-loga（|x|+1）在（0，+∞）上至少有三个零点，则a的取值范围是（　　）
A、（0，
2
2
）
B、（0，
3
3
）
C、（0，
5
5
）
D、（0，
6
6
）
直线L过A（1，1）与两坐标轴交于M、N两点，当L绕A旋转时，MN的中点轨迹方程为
 
．
数列0，1，0，-1，0，1，0，-1，…的一个通项公式是
 
．
若sin（α-β）cosα-cos（α-β）sinα=
4
5
，且β∈（π，
3
2
π），则cos 
β
2
为
 
．
设|
a
|=4，|
b
|=3，夹角为60°，则|
a
+
b
|等于（　　）
A、37
B、13
C、
37
D、
13
已知
a
，
b
为不共线的向量，设条件M：
b
⊥（
a
-
b
）；条件N：对一切x∈R，不等式|
a
-x
b
|≥|
a
-
b
|恒成立．则M是N的
 
条件．
过抛物线y=2x2的焦点F的直线与抛物线交于A、B两点，若|AF|=1，则|BF|=（　　）
A、
1
7
B、1
C、
1
3
D、7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网