题目内容
已知A(1,3),B(-1,0),求:
(Ⅰ)A,B两点间的距离;
(Ⅱ)线段AB的垂直平分线方程.
(Ⅰ)A,B两点间的距离;
(Ⅱ)线段AB的垂直平分线方程.
考点:两点间距离公式的应用
专题:计算题,直线与圆
分析:(Ⅰ)利用两点间距离公式,即可求出A,B两点间的距离;
(Ⅱ)求出斜率,线段AB的中点坐标,可得线段AB的垂直平分线方程.
(Ⅱ)求出斜率,线段AB的中点坐标,可得线段AB的垂直平分线方程.
解答:
解:(Ⅰ) |AB|=
=
. …4分
(Ⅱ)直线AB的斜率kAB=
=
,设线段AB的垂直平分线为l,
则l的斜率kl=-
=-
. …6分
线段AB的中点坐标为(
,
),即(0,
). …8分
由直线的点斜式方程得l的方程为y=-
x+
,即4x+6y-9=0.…10分
| (1+1)2+(3-0)2 |
| 13 |
(Ⅱ)直线AB的斜率kAB=
| 3-0 |
| 1-(-1) |
| 3 |
| 2 |
则l的斜率kl=-
| 1 |
| kAB |
| 2 |
| 3 |
线段AB的中点坐标为(
| 1-1 |
| 2 |
| 3+0 |
| 2 |
| 3 |
| 2 |
由直线的点斜式方程得l的方程为y=-
| 2 |
| 3 |
| 3 |
| 2 |
点评:本题考查两点间距离公式,考查直线方程,考查学生分析解决问题的能力,比较基础.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
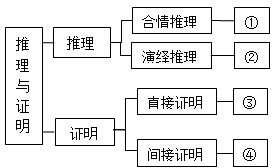 如图是选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“分析法”,则应该放在图( )
如图是选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“分析法”,则应该放在图( )| A、“①”处 | B、“②”处 |
| C、“③”处 | D、“④”处 |
二次函数f(x)=ax2+bx+c中,a>0且a≠1,对于任意的x∈R都有f(x-3)=f(1-x),设m=f(log
),n=f[(
)loga2],则( )
| a |
| 1 |
| a |
| 1 |
| a |
| A、m<n |
| B、m=n |
| C、m>n |
| D、m,n的大小关系不确定 |
过抛物线y=2x2的焦点F的直线与抛物线交于A、B两点,若|AF|=1,则|BF|=( )
A、
| ||
| B、1 | ||
C、
| ||
| D、7 |
下列推导错误的是( )
| A、α∥β,a?α⇒a∥β |
| B、a∥b,a⊥α⇒b⊥α |
| C、a∥b,b?α⇒a∥α |
| D、a⊥α,a?β⇒α⊥β |
执行如图所示的程序框图,当输出值为4时,输入x的值为( )


| A、2 | B、±2 |
| C、-2或-3 | D、2或-3 |
