题目内容
(1)求下列函数的导数
①y=x(x2+
+
); ②y=(
+1)(
-1);
(2)已知函数f(x)=3x+2cosx+sinx,且a=f′(
),f′(x)是f(x)的导函数,求过曲线y=x3上一点P(a,b)的切线方程.
①y=x(x2+
| 1 |
| x |
| 1 |
| x3 |
| x |
| 1 | ||
|
(2)已知函数f(x)=3x+2cosx+sinx,且a=f′(
| π |
| 2 |
考点:利用导数研究曲线上某点切线方程,导数的运算
专题:导数的综合应用
分析:(1)①利用单项式乘多项式化简,然后利用基本初等函数的导数公式化简;
②利用多项式乘多项式化简,然后利用基本初等函数的导数公式化简;
(2)求出函数f(x)的导函数,结合a=f′(
)求得a的值,把点P(a,b)代入y=x3求b的值,然后设出切点Q的坐标,求出切线方程,结合P的坐标求出切点坐标,则切线方程可求.
②利用多项式乘多项式化简,然后利用基本初等函数的导数公式化简;
(2)求出函数f(x)的导函数,结合a=f′(
| π |
| 2 |
解答:
解:(1)①y=x(x2+
+
)=x3+1+
,
∴y′=3x2-
;
②y=(
+1)(
-1)
•
-
+
-1=-x
+x
,
∴y′=-
x-
-
x-
=
(1+
);
(2)由f(x)=3x+2cosx+sinx,得f′(x)=3-2sinx+cosx,
则a=f′(
)=1,
∴P(1,1),
设切点Q(x0,y0),
又y′=3x2,
∴得切线斜率k=3x02,
∴曲线在点Q处的切线方程为:
y-x03=3x02(x-x0),
又切线过点P(1,1),
∴有1-x03=3x02(1-x0),整理得:(x0-1)(2x02-1)=0,
解得:x0=1或x0=
或x0=-
,
∴切线方程为:y=3x-2或y=
x±
.
| 1 |
| x |
| 1 |
| x3 |
| 1 |
| x2 |
∴y′=3x2-
| 2 |
| x3 |
②y=(
| x |
| 1 | ||
|
| x |
| 1 | ||
|
| x |
| 1 | ||
|
| 1 |
| 2 |
| 1 |
| 2 |
∴y′=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| -1 | ||
2
|
| 1 |
| x |
(2)由f(x)=3x+2cosx+sinx,得f′(x)=3-2sinx+cosx,
则a=f′(
| π |
| 2 |
∴P(1,1),
设切点Q(x0,y0),
又y′=3x2,
∴得切线斜率k=3x02,
∴曲线在点Q处的切线方程为:
y-x03=3x02(x-x0),
又切线过点P(1,1),
∴有1-x03=3x02(1-x0),整理得:(x0-1)(2x02-1)=0,
解得:x0=1或x0=
| ||
| 2 |
| ||
| 2 |
∴切线方程为:y=3x-2或y=
| 3 |
| 2 |
| ||
| 2 |
点评:本题考查了基本初等函数的导数公式,考查了利用导数研究过曲线上某点处的切线方程,是中档题.

练习册系列答案
相关题目
设|
|=4,|
|=3,夹角为60°,则|
+
|等于( )
| a |
| b |
| a |
| b |
| A、37 | ||
| B、13 | ||
C、
| ||
D、
|
质量m=2kg的物体作直线运动,运动距离s(单位:m)关于时间t(单位:s)的函数是s(t)=3t2+1,且物体的动能U=
mv2,则物体运动后第3s时的动能为( )
| 1 |
| 2 |
| A、18焦耳 | B、361焦耳 |
| C、342焦耳 | D、324焦耳 |
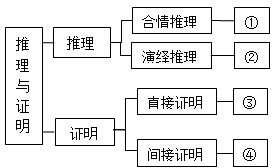 如图是选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“分析法”,则应该放在图( )
如图是选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“分析法”,则应该放在图( )| A、“①”处 | B、“②”处 |
| C、“③”处 | D、“④”处 |
