题目内容
设P:函数y=cx在R上单调递减,Q:函数y=x2+|x|+2c的最小值大于1.如果命题“p∨q”为真命题,且“p∧q”为假命题,求c的取值范围.
考点:复合命题的真假
专题:计算题,简易逻辑
分析:由命题“p∨q”为真命题,且“p∧q”为假命题可知p、q一真一假,分别讨论即可.
解答:
解:∵命题“p∨q”为真命题,且“p∧q”为假命题,
∴p、q一真一假,
若p真q假,则
解得,0<c≤
,
若p假q真,则
解得,c>1.
综上所述,0<c≤
或c>1.
∴p、q一真一假,
若p真q假,则
|
解得,0<c≤
| 1 |
| 2 |
若p假q真,则
|
解得,c>1.
综上所述,0<c≤
| 1 |
| 2 |
点评:本题考查了复合命题的真假及指数函数的单调性与二次函数的最值,属于基础题.

练习册系列答案
相关题目
质量m=2kg的物体作直线运动,运动距离s(单位:m)关于时间t(单位:s)的函数是s(t)=3t2+1,且物体的动能U=
mv2,则物体运动后第3s时的动能为( )
| 1 |
| 2 |
| A、18焦耳 | B、361焦耳 |
| C、342焦耳 | D、324焦耳 |
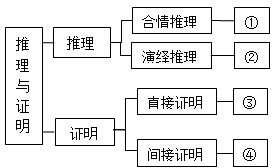 如图是选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“分析法”,则应该放在图( )
如图是选修1-2第二章“推理与证明”的知识结构图(部分),如果要加入知识点“分析法”,则应该放在图( )| A、“①”处 | B、“②”处 |
| C、“③”处 | D、“④”处 |
二次函数f(x)=ax2+bx+c中,a>0且a≠1,对于任意的x∈R都有f(x-3)=f(1-x),设m=f(log
),n=f[(
)loga2],则( )
| a |
| 1 |
| a |
| 1 |
| a |
| A、m<n |
| B、m=n |
| C、m>n |
| D、m,n的大小关系不确定 |
执行如图所示的程序框图,当输出值为4时,输入x的值为( )


| A、2 | B、±2 |
| C、-2或-3 | D、2或-3 |