题目内容
2.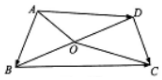 如图,在平面四边形ABCD中,O为BD的中点,且OA=3,OC=5,若$\overrightarrow{AB}$•$\overline{AD}$=-7,则$\overrightarrow{BC}$•$\overrightarrow{DC}$的值是9.
如图,在平面四边形ABCD中,O为BD的中点,且OA=3,OC=5,若$\overrightarrow{AB}$•$\overline{AD}$=-7,则$\overrightarrow{BC}$•$\overrightarrow{DC}$的值是9.
分析 根据平面向量的线性表示与数量积运算,利用$\overrightarrow{AB}$•$\overline{AD}$=($\overrightarrow{AO}$+$\overrightarrow{OB}$)•($\overrightarrow{AO}$+$\overrightarrow{OD}$)求出|$\overrightarrow{OB}$|=|$\overrightarrow{OD}$|=4;再利用$\overrightarrow{BC}$•$\overrightarrow{DC}$=($\overrightarrow{BO}$+$\overrightarrow{OC}$)•($\overrightarrow{DO}$+$\overrightarrow{OC}$)求出运算结果.
解答 解:平面四边形ABCD中,O为BD的中点,
且OA=3,OC=5,∴$\overrightarrow{OB}$+$\overrightarrow{OD}$=$\overrightarrow{0}$;
若$\overrightarrow{AB}$•$\overline{AD}$=-7,
则($\overrightarrow{AO}$+$\overrightarrow{OB}$)•($\overrightarrow{AO}$+$\overrightarrow{OD}$)=${\overrightarrow{AO}}^{2}$+$\overrightarrow{AO}$•$\overrightarrow{OD}$+$\overrightarrow{AO}$•$\overrightarrow{OB}$+$\overrightarrow{OB}$•$\overrightarrow{OD}$
=${\overrightarrow{AO}}^{2}$+$\overrightarrow{OA}$•($\overrightarrow{OD}$+$\overrightarrow{OB}$)-${\overrightarrow{OB}}^{2}$
=32-${\overrightarrow{OB}}^{2}$=-7;
∴${\overrightarrow{OB}}^{2}$=16,
∴|$\overrightarrow{OB}$|=|$\overrightarrow{OD}$|=4;
∴$\overrightarrow{BC}$•$\overrightarrow{DC}$=($\overrightarrow{BO}$+$\overrightarrow{OC}$)•($\overrightarrow{DO}$+$\overrightarrow{OC}$)
=$\overrightarrow{BO}$•$\overrightarrow{DO}$+$\overrightarrow{BO}$•$\overrightarrow{OC}$+$\overrightarrow{OD}$•$\overrightarrow{OC}$+${\overrightarrow{OC}}^{2}$
=-${\overrightarrow{BO}}^{2}$+$\overrightarrow{OC}$•($\overrightarrow{BO}$+$\overrightarrow{OD}$)+${\overrightarrow{OC}}^{2}$
=-42+0+52
=9.
点评 本题考查了平面向量的线性表示与数量积运算问题,是基础题.

| A. | -1+i | B. | -1-i | C. | 1-i | D. | 1+i |
| 分组(年龄) | [7,20) | [20,40) | [40,80) |
| 频数(人) | 18 | 54 | 36 |
(Ⅱ)在(Ⅰ)中抽出的6人中,任选2人参加一对一的对抗比赛,求这2人来自同一年龄组的概率.