题目内容
做投掷2颗骰子试验,用(x,y)表示点P的坐标,其中x表示第1颗骰子出现的点数,y表示第2颗骰子出现的点数.
(1)求点P在直线y=x上的概率;
(2)求点P的坐标(x,y)满足16<x2+y2≤25的概率.
(1)求点P在直线y=x上的概率;
(2)求点P的坐标(x,y)满足16<x2+y2≤25的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(1)每颗骰子出现的点数都有6种情况,所以基本事件总数为6×6=36个.记“点P在直线y=x上”为事件A,则事件A有6个基本事件,由此能求出点P在直线y=x上的概率.
(2)记记“点P坐标满足16<x2+y2≤25”为事件B,则事件B有7个基本事件.由此能求出点P的坐标(x,y)满足16<x2+y2≤25的概率.
(2)记记“点P坐标满足16<x2+y2≤25”为事件B,则事件B有7个基本事件.由此能求出点P的坐标(x,y)满足16<x2+y2≤25的概率.
解答:
解:(1)每颗骰子出现的点数都有6种情况,所以基本事件总数为6×6=36个.
记“点P在直线y=x上”为事件A,则事件A有6个基本事件,
即A={(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)},
∴P(A)=
=
.
(2)记记“点P坐标满足16<x2+y2≤25”为事件B,
则事件B有7个基本事件.
即B={(1,4),(2,4),(3,3),(3,4),(4,1),(4,2),(4,3)},
∴P(B)=
.
记“点P在直线y=x上”为事件A,则事件A有6个基本事件,
即A={(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)},
∴P(A)=
| 6 |
| 36 |
| 1 |
| 6 |
(2)记记“点P坐标满足16<x2+y2≤25”为事件B,
则事件B有7个基本事件.
即B={(1,4),(2,4),(3,3),(3,4),(4,1),(4,2),(4,3)},
∴P(B)=
| 7 |
| 36 |
点评:本题考查概率的求法,是中档题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
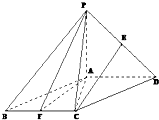 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,PA=BC=1,PD=AB=
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,平面PAD⊥平面ABCD,PA=BC=1,PD=AB=