题目内容
已知等差数列{an}，a1=1，公差d≠0，若a1，a2，a6成等比数列，则a11= ．
考点：等差数列的通项公式
专题：等差数列与等比数列
分析：由题意可得（1+d）2=1×（1+5d），解得d由等差数列的通项公式可得．
解答：
解：∵等差数列{an}，a1=1，公差d≠0，且a1，a2，a6成等比数列，
∴a22=a1•a6，代入数据可得（1+d）2=1×（1+5d），
解得d=3，或d=0（舍去）
∴a11=a1+10d=1+10×3=31
故答案为：31
∴a22=a1•a6，代入数据可得（1+d）2=1×（1+5d），
解得d=3，或d=0（舍去）
∴a11=a1+10d=1+10×3=31
故答案为：31
点评：本题考查等差数列的通项公式，涉及等比数列的通项公式，属基础题．
练习册系列答案
相关题目
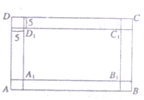某市政府为了打造宜居城市，计划在公园内新建一个如图所示的矩形ABCD的休闲区，内不是矩形景观区A1B1C1D1，景观区四周是人行道，已知景观区的面积为8000平方米，人行道的宽为5米（如图所示）．“m=1”是“?x∈（0，+∞），使得m≥x+
-1”的（ ）
| 1 |
| x |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知直线3x+4y-3=0与直线6x+my+14=0平行，则它们之间的距离是（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
| D、4 |
已知直线l过点P（3，2）．