题目内容

如图，在地面A处测得树梢的仰角为60°，A与树底部B相距为5米，则树高度（　　）
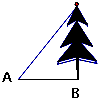
A、5
3
米
B、5米
C、10米
D、
5
3
3
米
考点：解三角形的实际应用
专题：解三角形
分析：直接利用解直角三角形求出树高度即可．
解答： 解：地面A处测得树梢的仰角为60°，A与树底部B相距为5米，则树高度：ABtan60°=5
3
．
故选：A．
点评：本题考查三角形的解法，三角函数的定义，基本知识的考查．
练习册系列答案
相关题目
已知a是方程3x2-4x+1=0的根，指数函数f（x）=ax若实数m＞n，则f（m），f（n）的大小关系为
 
．
若函数y=ax-（b+1）（a＞0，a≠1）的图象在第一、三、四象限，则有（　　）
A、a＞1且b＜1
B、a＞1且b＞0
C、0＜a＜1且b＞0
D、0＜a＜1且b＜0
下列命题中错误的是（　　）
A、|x+
1
x
|≥2(x≠0)
B、x2+
1
x2
≥2(x≠0)
C、
x2+2
x2+1
的最小值为2（x∈R）
D、
x2+4
x2+3
的最小值为2（x∈R）
等差数列{an}中，a1=1，a3+a5=14，前n项和Sn=100，求项数n的值．
已知f（x）=
2x2-8ax+3，x＜1
ax-a，x≥1
是R上的单调递减函数，则实数a的取值范围为（　　）
A、(0，
1
2
]
B、[
5
8
，1)
C、[
1
2
，
3
4
]
D、[
1
2
，
5
8
]
设函数f（x）=log2x．
（1）解不等式f（x-1）+f（x）＞1；
（2）设函数g（x）=f（2x+1）+kx，若函数g（x）为偶函数，求实数k的值；
（3）当x∈[t+2，t+3]时，是否存在实数t（其中0＜t＜1），使得不等式|f（
1
x-t
）-f（x-3t）|≤1恒成立？若存在，求出t的取值范围；若不存在，说明理由．
设f（x）是定义在实数集R上的函数，满足条件：y=f（x+1）是偶函数，且当x≥1时，f（x）=5x 则f（
2
3
），f（
3
2
），f（
1
3
）的大小关系是（　　）
A、f（
1
3
）＜f（
2
3
）＜f（
3
2
）
B、f（
3
2
）＜f（
1
3
）＜f（
2
3
）
C、f（
3
2
）＜f（
2
3
）＜f（
1
3
）
D、f（
2
3
）＜f（
3
2
）＜f（
1
3
）
已知函数f（x）=
2
kx2-4kx+k+3
的定义域为R，则k的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网