题目内容
已知f(x)=
是R上的单调递减函数,则实数a的取值范围为( )
|
A、(0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|
考点:函数单调性的性质
专题:函数的性质及应用
分析:结合二次函数,指数函数的性质,得到不等式组,解出即可.
解答:
解:由题意得:
,解得:
≤a≤
,
故选:D.
|
| 1 |
| 2 |
| 5 |
| 8 |
故选:D.
点评:本题考查了二次函数的性质,指数函数的性质,考查了函数的单调性,是一道中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
已知函数f(x)=cos
cos(
+2x),则函数f(x)满足( )
| 2π |
| 3 |
| π |
| 2 |
| A、f(x)的最小正周期是2π | ||||||||||||
| B、若f(x1)=f(x2),则x1=x2 | ||||||||||||
C、f(x)的图象关于直线x=
| ||||||||||||
D、当x∈[-
|
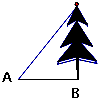
如图,在地面A处测得树梢的仰角为60°,A与树底部B相距为5米,则树高度( )

A、5
| ||||
| B、5米 | ||||
| C、10米 | ||||
D、
|
| ||||||||
(
|
| A、1 | ||
B、m
| ||
C、m
| ||
| D、m |