题目内容
设f(x)是定义在实数集R上的函数,满足条件:y=f(x+1)是偶函数,且当x≥1时,f(x)=5x 则f(
),f(
),f(
)的大小关系是( )
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
A、f(
| ||||||
B、f(
| ||||||
C、f(
| ||||||
D、f(
|
考点:函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:由y=f(x+1)是偶函数可得y=f(x)的图象关于x=1对称,从而转化到同一个单调区间内比较大小.
解答:
解:∵y=f(x+1)是偶函数,
∴y=f(x)的图象关于x=1对称,
∴f(
)=f(
),f(
)=f(
),
又∵当x≥1时,f(x)=5x,
∴f(
)<f(
)<f(
),
即f(
)<f(
)<f(
).
故选D.
∴y=f(x)的图象关于x=1对称,
∴f(
| 2 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 5 |
| 3 |
又∵当x≥1时,f(x)=5x,
∴f(
| 4 |
| 3 |
| 3 |
| 2 |
| 5 |
| 3 |
即f(
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 3 |
故选D.
点评:本题考查了函数的对称性与单调性的应用,属于基础题.

练习册系列答案
相关题目
以圆x2+2x+y2=0的圆心为圆心,半径为2的圆的方程是( )
| A、(x-1)2+y2=4 |
| B、(x-1)2+y2=2 |
| C、(x+1)2+y2=2 |
| D、(x+1)2+y2=4 |
如图,在地面A处测得树梢的仰角为60°,A与树底部B相距为5米,则树高度( )
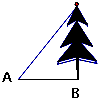

A、5
| ||||
| B、5米 | ||||
| C、10米 | ||||
D、
|
| ||||||||
(
|
| A、1 | ||
B、m
| ||
C、m
| ||
| D、m |
如果命题“p∨q”为真命题,则( )
| A、p,q中至少有一个为真命题 |
| B、p,q均为假命题 |
| C、p,q均为真命题 |
| D、p,q中至多有一个为真命题 |
在算式4×□+△=30的□、△中,分别填入一个正整数使算式成立,并使它们的倒数之和最小,则这两个数构成的数对(□、△)应为( )
| A、(4,14) |
| B、(6,6) |
| C、(3,18) |
| D、(5,10) |