题目内容
设x，y满足约束条件
，若目标函数z=ax+by（a＞0，b＞0）的最大值为6，则
+
的最小值为 ．
|
| 1 |
| 2a |
| 3 |
| b |
考点：简单线性规划
专题：数形结合,不等式的解法及应用
分析：由约束条件作出可行域，数形结合得到最优解，结合目标函数的最大值得到
+
=1，然后利用基本不等式求得
+
的最小值．
| a |
| 6 |
| b |
| 4 |
| 1 |
| 2a |
| 3 |
| b |
解答：
解：由约束条件
作出可行域如图，
化目标函数z=ax+by为y=-
x+
，
联立
，解得：C（1，
）．
由图可知，当直线y=-
x+
过C（1，
）时目标函数有最大值为6．
即a+
b=6．
则
+
=1．
∴
+
=(
+
)•(
+
)=
+
+
+
≥
+2
=
（当且仅当b=2a时等号成立）．
故答案为：
．
|
化目标函数z=ax+by为y=-
| a |
| b |
| z |
| b |
联立
|
| 3 |
| 2 |
由图可知，当直线y=-
| a |
| b |
| z |
| b |
| 3 |
| 2 |
即a+
| 3 |
| 2 |
则
| a |
| 6 |
| b |
| 4 |
∴
| 1 |
| 2a |
| 3 |
| b |
| 1 |
| 2a |
| 3 |
| b |
| a |
| 6 |
| b |
| 4 |
| 1 |
| 12 |
| 3 |
| 4 |
| b |
| 8a |
| a |
| 2b |
| 5 |
| 6 |
|
| 4 |
| 3 |
故答案为：
| 4 |
| 3 |
点评：本题考查了简单的线性规划，考查了数形结合的解题思想方法，训练了基本不等式求最值，是中档题．
练习册系列答案
相关题目
双曲线
-
=1的两个焦点为F1（-5，0），F2（5，0），其上一点M满足MF1-MF2=-8，则该双曲线的一条渐近线方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、4x+3y=0 |
| B、4x-5y=0 |
| C、3x-4y=0 |
| D、5x+3y=0 |
设函数f（x）=
，若f（a）＞f（-a），则实数a的取值范围是（ ）
|
| A、（-1，0）∪（1，+∞） |
| B、（-∞，-1） |
| C、（1，+∞） |
| D、（-∞，-1）∪（1，+∞） |
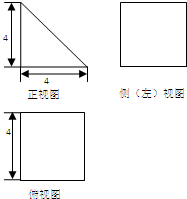一个空间几何体的三视图如图所示，其中正视图为等腰直角三角形，侧视图与俯视图为正方形，则该几何体的表面积为