题目内容
已知f(x)=x3-ax2+3x,g(x)=lnx+b
(Ⅰ)若曲线h(x)=
+g(x)在x=1处的切线是x+y=0,求实数a和b的值;
(Ⅱ)若x=3是f(x)的极值点,求f(x)在[0,2]上的最大最小值.
(Ⅰ)若曲线h(x)=
| f(x) |
| x |
(Ⅱ)若x=3是f(x)的极值点,求f(x)在[0,2]上的最大最小值.
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:计算题,导数的综合应用
分析:(Ⅰ)h(x)=
+g(x)=x2-ax+3+lnx+b,求导h′(x)=2x-a+
;从而可得
,从而解得;
(Ⅱ)f′(x)=3x2-2ax+3,由题意可得3×32-6a+3=0从而解出a,列表得到函数的最值.
| f(x) |
| x |
| 1 |
| x |
|
(Ⅱ)f′(x)=3x2-2ax+3,由题意可得3×32-6a+3=0从而解出a,列表得到函数的最值.
解答:
解:(Ⅰ)∵h(x)=
+g(x)=x2-ax+3+lnx+b,
∴h′(x)=2x-a+
;
∵在x=1处的切线是x+y=0,
∴
,
解得,a=4,b=-1;
(Ⅱ)f′(x)=3x2-2ax+3,
∵x=3是f(x)的极值点,
∴f′(3)=3×32-6a+3=0,
解得a=5;
故f(x)=x3-5x2+3x,f′(x)=3x2-10x+3,
经检验成立;
在[0,2]列出x,f(x),f′(x)如下表,
函数f(x)在x=
处有最大值
;
在x=2处有最小值-6.
| f(x) |
| x |
∴h′(x)=2x-a+
| 1 |
| x |
∵在x=1处的切线是x+y=0,
∴
|
解得,a=4,b=-1;
(Ⅱ)f′(x)=3x2-2ax+3,
∵x=3是f(x)的极值点,
∴f′(3)=3×32-6a+3=0,
解得a=5;
故f(x)=x3-5x2+3x,f′(x)=3x2-10x+3,
经检验成立;
在[0,2]列出x,f(x),f′(x)如下表,
| x | 0 | (0,
|
| (
| 2 | ||||||
| f′(x) | + | 0 | - | ||||||||
| f(x) | 0 | 上升 | 极大值
| 下降 | -6 |
| 1 |
| 3 |
| 13 |
| 27 |
在x=2处有最小值-6.
点评:本题考查了导数的综合应用及闭区间上的最值,属于中档题.

练习册系列答案
相关题目
与命题“若p则q”的否命题真假相同的命题是( )
| A、若q 则p |
| B、若¬p则q |
| C、若¬q则p |
| D、若¬p则¬q |
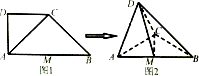 如图1,在四边形ABCD中,AD⊥CD,CD∥AB,AB=2AD=2CD=4,M为线段AB的中点,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2,所示.
如图1,在四边形ABCD中,AD⊥CD,CD∥AB,AB=2AD=2CD=4,M为线段AB的中点,将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D-ABC,如图2,所示.