题目内容
已知函数f(x)=lg(x-1),g(x)=lg(x2+1)
(1)求f(x)和g(x)的定义域;
(2)判断g(x)奇偶性,并证明你的结论;
(3)判断f(x)在其定义域上的单调性?并证明你的结论.
(1)求f(x)和g(x)的定义域;
(2)判断g(x)奇偶性,并证明你的结论;
(3)判断f(x)在其定义域上的单调性?并证明你的结论.
考点:函数的定义域及其求法,函数奇偶性的判断
专题:计算题,函数的性质及应用
分析:(1)由函数的定义域的求法,对数的真数必须大于0,解不等式即可得到定义域;
(2)运用函数的奇偶性的定义,注意判断定义域是否关于原点对称,再计算f(-x);
(3)运用函数的单调性的定义,注意作差、变形、定符号、下结论几个步骤.
(2)运用函数的奇偶性的定义,注意判断定义域是否关于原点对称,再计算f(-x);
(3)运用函数的单调性的定义,注意作差、变形、定符号、下结论几个步骤.
解答:
解:(1)由于函数f(x)=lg(x-1),则x-1>0,即x>1,定义域为(1,+∞),
由于g(x)=lg(x2+1),则x2+1>0,即x∈R,则定义域为R;
(2)g(x)在R上是偶函数.
理由如下:定义域为R,关于原点对称,
g(-x)=lg[(-x)2+1]=g(x),则g(x)在R上是偶函数;
(3)f(x)在(1,+∞)上为增函数.
理由如下:令1<m<n,则f(m)-f(n)=lg(m-1)-lg(n-1)
=lg
,由于
-1=
,又1<m<n,则m-n<0,n-1>0,
即有由于
<1,则lg
<0,即有f(m)<f(n),
则有f(x)在(1,+∞)上为增函数.
由于g(x)=lg(x2+1),则x2+1>0,即x∈R,则定义域为R;
(2)g(x)在R上是偶函数.
理由如下:定义域为R,关于原点对称,
g(-x)=lg[(-x)2+1]=g(x),则g(x)在R上是偶函数;
(3)f(x)在(1,+∞)上为增函数.
理由如下:令1<m<n,则f(m)-f(n)=lg(m-1)-lg(n-1)
=lg
| m-1 |
| n-1 |
| m-1 |
| n-1 |
| m-n |
| n-1 |
即有由于
| m-1 |
| n-1 |
| m-1 |
| n-1 |
则有f(x)在(1,+∞)上为增函数.
点评:本题考查函数的性质和运用,考查函数的定义域的求法,函数的奇偶性的判断和单调性的判断,注意运用定义,属于基础题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
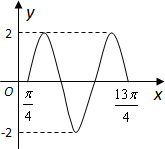 在研究性学习中,我校高三某班的一个课题研究小组做“关于横波的研究实验”.根据实验记载,他们观察到某一时刻的波形曲线符合函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=
在研究性学习中,我校高三某班的一个课题研究小组做“关于横波的研究实验”.根据实验记载,他们观察到某一时刻的波形曲线符合函数f(x)=2sin(ωx+φ)的图象,其部分图象如图所示,则f(0)=