题目内容
正四面体ABCD的外接球的体积为4
π,则正四面体ABCD的体积是 .
| 3 |
考点:棱柱、棱锥、棱台的体积
专题:计算题,空间位置关系与距离
分析:设正四面体的棱长为x,求出正四面体的高,由于外接球的体积为4
π,运用体积公式,解得r=
,利用勾股定理求出x的值,运用棱锥的体积公式,可求正四面体ABCD的体积.
| 3 |
| 3 |
解答:
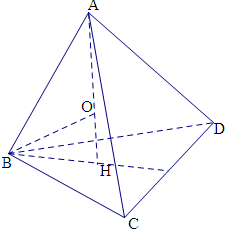 解:设正四面体的棱长为x,
解:设正四面体的棱长为x,
则底面三角形的高为
x,即有BH=
×
x=
x,
棱锥的高为AH=
=
=
x,
由于外接球的体积为4
π,即有
πr3=4
π,解得r=
,
在直角三角形BOH,得BO2=BH2+OH2,
即有r2=(
x-r)2+(
x)2,解得x=
r=2
,
则正四面体ABCD的体积为
×AH•S△BCD=
×
×2
×
×(2
)2=
故答案为:
 解:设正四面体的棱长为x,
解:设正四面体的棱长为x,则底面三角形的高为
| ||
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
棱锥的高为AH=
| AB2-BH2 |
x2-
|
| ||
| 3 |
由于外接球的体积为4
| 3 |
| 4 |
| 3 |
| 3 |
| 3 |
在直角三角形BOH,得BO2=BH2+OH2,
即有r2=(
| ||
| 3 |
| ||
| 3 |
2
| ||
| 3 |
| 2 |
则正四面体ABCD的体积为
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
| 2 |
| ||
| 4 |
| 2 |
| 8 |
| 3 |
故答案为:
| 8 |
| 3 |
点评:本题考查球的内接多面体的知识,考查计算能力,逻辑思维能力,是中档题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
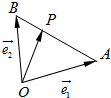 设
设| OA |
| e1 |
| OB |
| e2 |
| e1 |
| e2 |
| OP |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
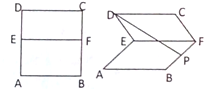 已知E,F是正方形ABCD的边AD,BC中点,P是BF的中点,如图将该正方形以EF为棱折成60°的二面角D-EF-A,则直线DP和平面ABFE所成角的正切值是
已知E,F是正方形ABCD的边AD,BC中点,P是BF的中点,如图将该正方形以EF为棱折成60°的二面角D-EF-A,则直线DP和平面ABFE所成角的正切值是