题目内容
已知A={x|2≤x≤4},定义在A上的函数f(x)=logax(a>1)的最大值比最小值大1,求a的值.
考点:对数函数的值域与最值
专题:函数的性质及应用
分析:由于a>1,可得函数f(x)=logax在x∈A={x|2≤x≤4}上单调递增,因此当x=4时,函数f(x)取得最大值;
当x=2时,函数f(x)取得最小值.再利用对数的运算性质即可得出.
当x=2时,函数f(x)取得最小值.再利用对数的运算性质即可得出.
解答:
解:∵a>1,
∴函数f(x)=logax在x∈A={x|2≤x≤4}上单调递增,
∵定义在A上的函数f(x)=logax(a>1)的最大值比最小值大1,
∴f(4)-f(2)=loga4-loga2=1,∴loga2=1,
∴a=2.
∴函数f(x)=logax在x∈A={x|2≤x≤4}上单调递增,
∵定义在A上的函数f(x)=logax(a>1)的最大值比最小值大1,
∴f(4)-f(2)=loga4-loga2=1,∴loga2=1,
∴a=2.
点评:本题考查了对数函数的单调性及其运算性质,属于基础题.

练习册系列答案
相关题目
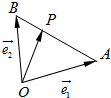 设
设| OA |
| e1 |
| OB |
| e2 |
| e1 |
| e2 |
| OP |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|