题目内容
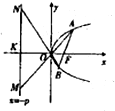 如图,过抛物线C:y2=2px的焦点F与x轴不垂直的直线交抛物线C与A、B两点,直线AO、BO分别与直线m:x=-p相交于M、N两点,则
如图,过抛物线C:y2=2px的焦点F与x轴不垂直的直线交抛物线C与A、B两点,直线AO、BO分别与直线m:x=-p相交于M、N两点,则| S△ABO |
| S△MNO |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设直线AB方程为y=k(x-
),代入y2=2px整理,表示出△ABO与△MNO的面积之比,即可得出结论.
| p |
| 2 |
解答:
解:设直线AB方程为y=k(x-
),
设M(-p,ym),N(-p,yn),A(x1,y1),B(x2,y2),
y=k(x-
)代入y2=2px整理得k2x2-(2p+2k2)x+
=0,
∴x1•x2=
.
∵A(x1,y1),B(x2,y2)在过抛物线C:y2=2px上,
得y1=
,y2=-
,
∴
•
=x1x2-2p
,
∵直线AO、BO分别与直线m:x=-p相交于M、N两点,
∴ym=-
•p,yn=
•p,
•
=p2-
,
∴
=
=
•
=
=
=
.
故选:C.
| p |
| 2 |
设M(-p,ym),N(-p,yn),A(x1,y1),B(x2,y2),
y=k(x-
| p |
| 2 |
| k2p2 |
| 4 |
∴x1•x2=
| p2 |
| 4 |
∵A(x1,y1),B(x2,y2)在过抛物线C:y2=2px上,
得y1=
| 2px1 |
| 2px2 |
∴
| OA |
| OB |
| x1x2 |
∵直线AO、BO分别与直线m:x=-p相交于M、N两点,
∴ym=-
|
|
| OM |
| ON |
| 2p3 | ||
|
∴
| S△ABO |
| S△MNO |
| ||
|
| AO |
| MO |
| BO |
| NO |
x1x2-2p
| ||||
p2-
|
| x1x2 |
| p2 |
| 1 |
| 4 |
故选:C.
点评:本题考查直线与抛物线的关系,考查学生的计算能力,属于中档题..

练习册系列答案
相关题目
已知命题p:?x∈R,cosx≥a,下列的取值能使“¬p”命题是真命题的是( )
| A、a∈R | B、a=2 |
| C、a=1 | D、a=0 |
圆(x-1)2+(y+2)2=20在x轴上截得的弦长是( )
| A、8 | ||
| B、6 | ||
C、6
| ||
D、4
|
若已知△ABC的周长为9,且a:b:c=3:2:4,则cosC的值为( )
A、-
| ||
B、
| ||
C、-
| ||
D、
|
在极坐标系中,直线ρsin(θ+
)=2,被圆ρ=3截得的弦长为( )
| π |
| 4 |
A、2
| ||
| B、2 | ||
C、2
| ||
D、2
|
对于函数f(x),若存在区间[m,n](m<n),使得f(x)在区间[m,n]上的值域为[λm,λn],则称f(x)为“λ倍函数”,若f(x)=ax(a>1)为“1倍函数”,则a的取值范围为( )
A、(1,
| ||
B、(
| ||
C、(1,e
| ||
D、(e
|
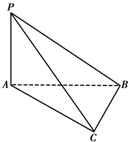 如图所示,已知PA垂直于△ABC所在平面,且∠ACB=90°,连结PB、PC,则图形中互相垂直的平面有( )
如图所示,已知PA垂直于△ABC所在平面,且∠ACB=90°,连结PB、PC,则图形中互相垂直的平面有( )| A、一对 | B、两对 | C、三对 | D、四对 |