题目内容
18.已知点A(0,-6),B(1,-5),且D为线段AB的中点.(Ⅰ)求中点D的坐标;
(Ⅱ)求线段AB的垂直平分线的方程.
分析 (Ⅰ)由已知条件求出AB的中点坐标为($\frac{1}{2}$,-$\frac{11}{2}$),(Ⅱ)求出kAB=1,由此能求出线段AB的垂直平分线的方程.
解答 解:(Ⅰ)∵A(0,-6),B(1,-5),
∴AB的中点D坐标为($\frac{1}{2}$,-$\frac{11}{2}$),
(Ⅱ)kAB=$\frac{-5+6}{1-0}$=1,
∴线段AB的垂直平分线的斜率是-1,
∴线段AB的垂直平分线的方程为:
y+$\frac{11}{2}$=-(x-$\frac{1}{2}$),
整理,得x+y+5=0.
点评 本题考查线段AB的垂直平分线的方程的求法,是基础题,解题时要注意中点坐标公式和直线与直线垂直的性质的合理运用.

练习册系列答案
相关题目
8.已知命题p:“?x∈R,x+1≥0”的否定是“?x∈R,x+1<0”;命题q:函数y=x-3是幂函数,则下列命题为真命题的是( )
| A. | p且q | B. | p或q | C. | ¬q | D. | p且(¬q) |
6.已知集合M={0,1,2,3,4},N={1,3,5},P=M∩N,则P的子集共有( )
| A. | 2 个 | B. | 3个 | C. | 4个 | D. | 5个 |
3.函数y=sinx的最小正周期是( )
| A. | π | B. | 2π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
7.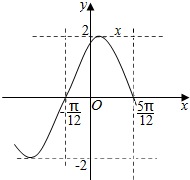 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )
 已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )
已知函数f(x)=Asin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(π)=( )| A. | $\sqrt{3}$ | B. | 0 | C. | -2 | D. | 1 |
8.过点($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),且与圆x2+y2=1相切的直线方程是( )
| A. | y=x+$\sqrt{2}$ | B. | y=-x+$\sqrt{2}$ | C. | y=x-$\sqrt{2}$ | D. | y=-x-$\sqrt{2}$ |
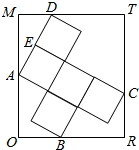 如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3.
如图,矩形ORTM内放置5个边长均为$\sqrt{3}$的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则($\overrightarrow{AE}$-$\overrightarrow{BC}$)•$\overrightarrow{BD}$=-3.